
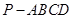 中,顶点
中,顶点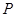 在底面
在底面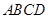 内的射影恰好落在
内的射影恰好落在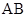 的中点
的中点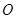 上,又
上,又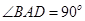 ,
,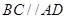 且
且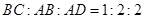
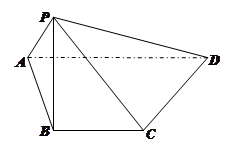
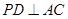 ;
;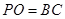 ,求直线
,求直线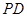 与
与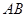 所成角的余弦值;
所成角的余弦值;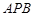 与平面
与平面 所成的角为
所成的角为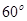 ,求
,求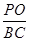 的值。
的值。 ;(3)
;(3)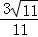 .
.
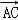 =(2a,a,0),
=(2a,a,0),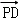 =(﹣a,2a,﹣h),
=(﹣a,2a,﹣h),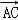 •
•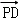 =﹣2a2+2a2=0,∴PD⊥AC; 4分
=﹣2a2+2a2=0,∴PD⊥AC; 4分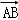 =(2a, 0,0),
=(2a, 0,0),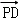 =(﹣a,2a,﹣a),
=(﹣a,2a,﹣a),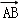 •
• =﹣2a2,cos<
=﹣2a2,cos<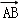 ,
, >=
>= =
= ,
, ; -8分
; -8分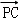 =(a,a,﹣h),
=(a,a,﹣h), =(﹣a,2a,﹣h),
=(﹣a,2a,﹣h), ,解得n=(1,2,
,解得n=(1,2, ),∴m•n=2,
),∴m•n=2, ,∵二面角为60°,∴
,∵二面角为60°,∴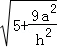 =4,
=4,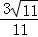 ,即
,即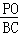 =
=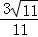 . 12分
. 12分

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
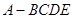 中,
中,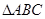 是正三角形,四边形
是正三角形,四边形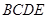 是矩形,且平面
是矩形,且平面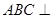 平面
平面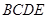 ,
,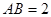 ,
,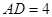 .
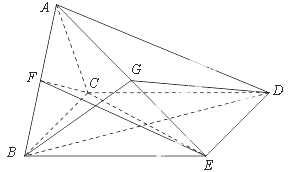
.
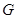 是
是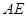 的中点,求证:
的中点,求证: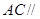 平面
平面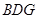 ;
;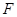 在线段
在线段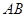 上什么位置时,二面角
上什么位置时,二面角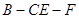 的余弦值为
的余弦值为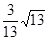 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
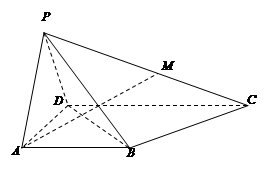
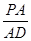 多大时,AM⊥平面PDB可能成立?
多大时,AM⊥平面PDB可能成立?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com