
已知函数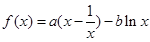 (
(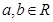 ),
),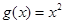 .
.
(Ⅰ)若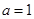 ,曲线
,曲线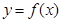 在点
在点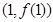 处的切线与
处的切线与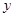 轴垂直,求
轴垂直,求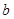 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,求证: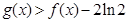 ;
;
(Ⅲ)若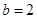 ,试探究函数
,试探究函数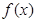 与
与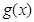 的图象在其公共点处是否存在公切线,若存在,研究
的图象在其公共点处是否存在公切线,若存在,研究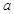 值的个数;若不存在,请说明理由.
值的个数;若不存在,请说明理由.
(Ⅰ)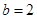 (Ⅱ)见解析(Ⅲ)当
(Ⅱ)见解析(Ⅲ)当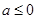 时,函数
时,函数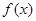 与
与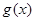 的图象在其公共点处不存在公切线;当
的图象在其公共点处不存在公切线;当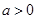 时,函数
时,函数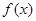 与
与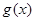 的图象在其公共点处存在公切线,且符合题意的
的图象在其公共点处存在公切线,且符合题意的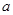 值有且仅有两个
值有且仅有两个
【解析】(I)当a=1时,根据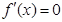 建立关于b的方程,求出b值.
建立关于b的方程,求出b值.
(II)由(I)得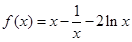 ,定义域为
,定义域为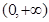 ,要证
,要证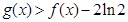 ,
,
只须证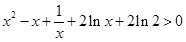 ,然后构造函数
,然后构造函数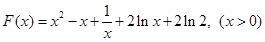 ,
,
利用导数研究其最小值,证明最小值大于零即可.
(III)本小题属于探索性问题,先假设函数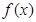 与
与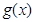 的图象在其公共点
的图象在其公共点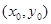 处存在公切线,则满足
处存在公切线,则满足
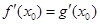 ,所以
,所以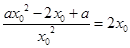 ,即
,即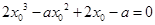 ,从而求出
,从而求出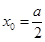 ,
,
然后再讨论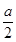 是否大于零来确定假设是否成立.
是否大于零来确定假设是否成立.
解:(Ⅰ)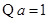 ,
,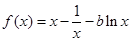 ,
,
∴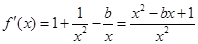 ,
--------------------------2分
,
--------------------------2分
依题意得 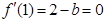 ,∴
,∴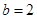 .
--------------------------3分
.
--------------------------3分
(Ⅱ)由(Ⅰ)得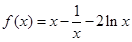 ,定义域为
,定义域为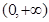 ,
,
要证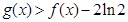 ,只须证
,只须证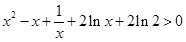 ,
,
设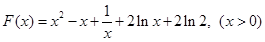 , -------------------4分
, -------------------4分
则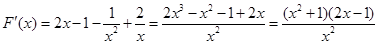 ,
,
令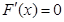 ,得
,得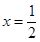 , ---------------------------6分
, ---------------------------6分
列表得
|
|
|
|
|
|
|
|
|
|
|
|
递减 |
极小 |
递增 |
∴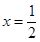 时,
时,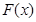 取极小值也是最小值,且
取极小值也是最小值,且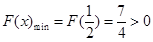 ,
,
∴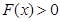 ,∴
,∴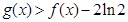 . --------------------8分
. --------------------8分
(Ⅲ)假设函数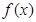 与
与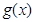 的图象在其公共点
的图象在其公共点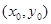 处存在公切线,
处存在公切线,
∵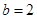 ,∴
,∴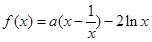 ,
,
∵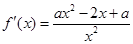 ,
,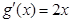 ,由
,由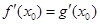 得,
得,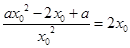 ,
,
即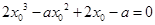 ,∴
,∴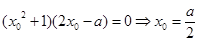 ,--------------9分
,--------------9分
∵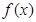 的定义域为
的定义域为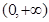 ,
,
当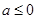 时,
时,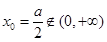 ,∴函数
,∴函数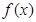 与
与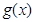 的图象在其公共点处不存在公切线;---10分
的图象在其公共点处不存在公切线;---10分
当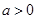 时,令
时,令 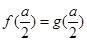 ,∵
,∵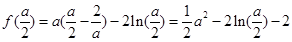 ,
,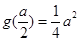 ,
,
∴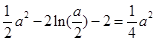 ,即
,即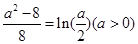 , ----------------11分
, ----------------11分
下面研究满足此等式的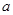 值的个数:
值的个数:
(方法一)由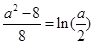 得
得 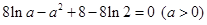 ,
,
设函数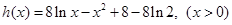 ,
,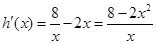 ,
,
令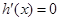 得
得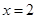 ,当
,当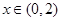 时,
时,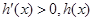 递增;
递增;
当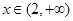 时,
时,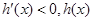 递减;
递减;
所以,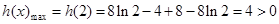 ,又
,又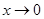 时,
时,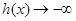 ,
,
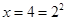 时,
时,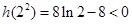 ,
,
所以,函数 的图象与
的图象与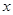 轴有且仅有两个交点,即符合题意的
轴有且仅有两个交点,即符合题意的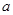 值有且仅有两个.
值有且仅有两个.
综上,当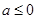 时,函数
时,函数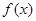 与
与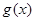 的图象在其公共点处不存在公切线;
的图象在其公共点处不存在公切线;
当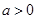 时,函数
时,函数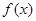 与
与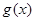 的图象在其公共点处存在公切线,
的图象在其公共点处存在公切线,
且符合题意的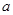 值有且仅有两个.-------------------------------14分
值有且仅有两个.-------------------------------14分
(方法二)设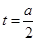 ,则
,则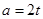 ,且
,且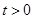 ,方程
,方程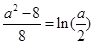 化为
化为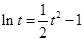 ,
,
分别画出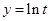 和
和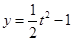 的图象,因为
的图象,因为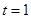 时,
时,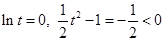 ,
,
由函数图象性质可得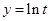 和
和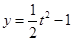 图象有且只有两个公共点(且均符合
图象有且只有两个公共点(且均符合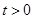 ),
),
所以方程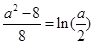 有且只有两个解.
有且只有两个解.
综上,当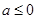 时,函数
时,函数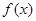 与
与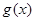 的图象在其公共点处不存在公切线;
的图象在其公共点处不存在公切线;
当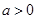 时,函数
时,函数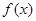 与
与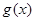 的图象在其公共点处存在公切线,
的图象在其公共点处存在公切线,
且符合题意的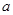 值有且仅有两个.--------------------------------14分
值有且仅有两个.--------------------------------14分


 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| π |
| 24 |
| 5π |
| 24 |
| π |
| 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 11π |
| 6 |
| ||
| 2 |
| 3 |
| π |
查看答案和解析>>
科目:高中数学 来源: 题型:
| xn+2 | xn-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com