
【题目】如图,四边形CDEF是正方形,四边形ABCD为直角梯形,∠ADC=90°,AB∥DC,平面CDEF⊥平面ABCD,AB=AD![]() CD=a,M在FB上,且BD∥平面ECM.
CD=a,M在FB上,且BD∥平面ECM.

(1)求证:M为BF中点;
(2)求证:平面BCF⊥平面EMC;
(3)求直线CD与平面ECM所成角的正弦值.
【答案】(1)见解析(2)见解析(3)![]() .
.
【解析】
(1)连结![]() ,
,![]() ,交于点
,交于点![]() ,则
,则![]() 是
是![]() 中点,连结
中点,连结![]() ,由
,由![]() 平面
平面![]() ,得
,得![]() ,由此能证明
,由此能证明![]() 为
为![]() 中点;
中点;
(2)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,利用向量法能证明平面
轴,建立空间直角坐标系,利用向量法能证明平面![]() 平面
平面![]() ;
;
(3)求出![]() ,
,![]() ,
,![]() ,平面
,平面![]() 的法向量
的法向量![]() ,1,
,1,![]() ,利用向量法能求出直线
,利用向量法能求出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)证明:连结DF,CE,交于点O,则O是DF中点,连结OM,
∴BD∥平面ECM,OM平面BDF,
∴BD∥OM,∴M为BF中点.
(2)证明:以D为原点,DA为x轴,DC为y轴,DE为z轴,建立空间直角坐标系,
则B(a,a,0),C(0,2a,0),F(0,2a,2a),M(![]() ),E(0,0,2a),
),E(0,0,2a),
![]() (﹣a,a,0),
(﹣a,a,0),![]() (﹣a,a,2a),
(﹣a,a,2a),![]() (
(![]() ,
,![]() ,﹣a),
,﹣a),![]() (0,2a,﹣2a),
(0,2a,﹣2a),
设平面BCF的法向量![]() (x,y,z),
(x,y,z),
则 ,取x=1,得
,取x=1,得![]() (1,1,0),
(1,1,0),
设平面EMC的法向量![]() (x1,y1,z1),
(x1,y1,z1),
则 ,取z1=1,得
,取z1=1,得![]() (﹣1,1,1),
(﹣1,1,1),
∵![]() 0,∴平面BCF⊥平面EMC.
0,∴平面BCF⊥平面EMC.
(3)解:D(0,0,0),![]() (0,﹣2a,0),平面EMC的法向量
(0,﹣2a,0),平面EMC的法向量![]() (﹣1,1,1),
(﹣1,1,1),
设直线CD与平面ECM所成角为θ,
则直线CD与平面ECM所成角的正弦值为:
sinθ .
.



科目:高中数学 来源: 题型:
【题目】在流行病学调查中,潜伏期指自病原体侵入机体至最早临床症状出现之间的一段时间.某地区一研究团队从该地区500名A病毒患者中,按照年龄是否超过60岁进行分层抽样,抽取50人的相关数据,得到如下表格:
潜伏期(单位:天) |
|
|
|
|
|
|
| |
人 数 | 60岁及以上 | 2 | 5 | 8 | 7 | 5 | 2 | 1 |
60岁以下 | 0 | 2 | 2 | 4 | 9 | 2 | 1 | |
(1)估计该地区500名患者中60岁以下的人数;
(2)以各组的区间中点值为代表,计算50名患者的平均潜伏期(精确到0.1);
(3)从样本潜伏超过10天的患者中随机抽取两人,求这两人中恰好一人潜伏期超过12天的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
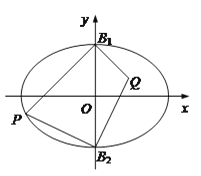
【题目】如图,在平面直角坐标系xOy中,B1,B2是椭圆![]() 的短轴端点,P是椭圆上异于点B1,B2的一动点.当直线PB1的方程为
的短轴端点,P是椭圆上异于点B1,B2的一动点.当直线PB1的方程为![]() 时,线段PB1的长为
时,线段PB1的长为![]() .
.
(1)求椭圆的标准方程;
(2)设点Q满足: ![]()
![]() .求证:△PB1B2与△QB1B2的面积之比为定值.
.求证:△PB1B2与△QB1B2的面积之比为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在△ABC中,∠A,∠B,∠C所对边分别为a,b,c,且bsinC+2csinBcosA=0.
(1)求∠A大小;
(2)若a=2![]() ,c=2,求△ABC的面积S的大小.
,c=2,求△ABC的面积S的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行横道时,应当减速慢行;遇行人正在通过人行横道,应当停车让行,俗称“礼让斑马线”,《中华人民共和国道路交通安全法》 第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼 让斑马线”行为统计数据:

(1)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该路口 9月份的不“礼让斑马线”违章驾驶员人数;
(3)若从表中3、4月份分别抽取4人和2人,然后再从中任选2 人进行交规调查,求抽到的两人恰好来自同一月份的概率.
参考公式: 
 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 且x,
且x,![]() .
.
(1)判断![]() 的奇偶性,并用定义证明;
的奇偶性,并用定义证明;
(2)若不等式![]() 在
在![]() 上恒成立,试求实数a的取值范围;
上恒成立,试求实数a的取值范围;
(3)![]() 的值域为
的值域为![]() 函数
函数![]() 在
在![]() 上的最大值为M,最小值为m,若
上的最大值为M,最小值为m,若![]() 成立,求正数a的取值范围.
成立,求正数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 定义在实数集
定义在实数集![]() 上的函数,把方程
上的函数,把方程![]() 称为函数
称为函数![]() 的特征方程,特征方程的两个实根
的特征方程,特征方程的两个实根![]() ,
,![]()
![]() 称为
称为![]() 的特征根.
的特征根.
(1)讨论函数的奇偶性,并说明理由;
(2)求![]() 表达式;
表达式;
(3)把函数![]() ,
,![]() 的最大值记作
的最大值记作![]() 、最小值记作
、最小值记作![]() ,令
,令![]() ,若
,若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 经过点
经过点![]() ,且和直线
,且和直线![]() 相切.
相切.
(Ⅰ)求该动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,若斜率为1的直线
,若斜率为1的直线![]() 与线段
与线段![]() 相交(不经过坐标原点
相交(不经过坐标原点![]() 和点
和点![]() ),且与曲线
),且与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定一个![]() 项的实数列
项的实数列![]() ,
, ![]() ,
, ![]() ,
, ![]() ,任意选取一个实数
,任意选取一个实数![]() ,变换
,变换![]() 将数列
将数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 变换为数列
变换为数列![]() ,
, ![]() ,
, ![]() ,
, ![]() ,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数
,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数![]() 可以不相同,第
可以不相同,第![]() 次变换记为
次变换记为![]() ,其中
,其中![]() 为第
为第![]() 次变换时所选择的实数.如果通过
次变换时所选择的实数.如果通过![]() 次变换后,数列中的各项均为
次变换后,数列中的各项均为![]() ,则称
,则称![]() ,
, ![]() ,
, ![]() ,
, ![]() 为“
为“![]() 次归零变换”.
次归零变换”.
(![]() )对数列
)对数列![]() ,
, ![]() ,
, ![]() ,
, ![]() ,给出一个“
,给出一个“![]() 次归零变换”,其中
次归零变换”,其中![]() .
.
(![]() )对数列
)对数列![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,给出一个“
,给出一个“![]() 次归零变换”,其中
次归零变换”,其中![]() .
.
(![]() )证明:对任意
)证明:对任意![]() 项的实数列,都存在“
项的实数列,都存在“![]() 次归零变换”.
次归零变换”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com