
 +
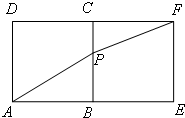
+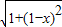 (0≤x≤1)的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC点P是边BC上的一动点,设CP=x,则AP+PF=f(x),请你参考这些信息,推知函数g(x)=4f(x)-9的零点的个数是 .
(0≤x≤1)的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC点P是边BC上的一动点,设CP=x,则AP+PF=f(x),请你参考这些信息,推知函数g(x)=4f(x)-9的零点的个数是 .
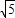 <
< ,当P与B或C重合时,f(x)取得最大值为
,当P与B或C重合时,f(x)取得最大值为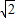 +1>
+1> .g(x)=4f(x)-9的零点的个数就是f(x)=
.g(x)=4f(x)-9的零点的个数就是f(x)= 的解的个数,而由题意可得 f(x)=
的解的个数,而由题意可得 f(x)= 的解有2个,从而得出结论.
的解有2个,从而得出结论.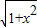 +
+ =AP+PF,当A、P、F共线 时,f(x)取得最小值为
=AP+PF,当A、P、F共线 时,f(x)取得最小值为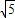 <
< ,当P与B或C重合时,f(x)取得最大值为
,当P与B或C重合时,f(x)取得最大值为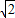 +1>
+1> .
. .故函数g(x)=4f(x)-9的零点的个数就是f(x)=
.故函数g(x)=4f(x)-9的零点的个数就是f(x)= 的解的个数.
的解的个数. 的解有2个,
的解有2个,

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:
 (2013•青岛二模)一同学为研究函数f(x)=
(2013•青岛二模)一同学为研究函数f(x)=| 1+x2 |
| 1+(1-x)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 一同学为研究函数f(x)=
一同学为研究函数f(x)=| 1+x2 |
| 1+(1-x)2 |
查看答案和解析>>
科目:高中数学 来源:青岛二模 题型:填空题
| 1+x2 |
| 1+(1-x)2 |
查看答案和解析>>
科目:高中数学 来源:2012年江苏省盐城中学高考数学二模试卷(解析版) 题型:解答题
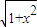 +
+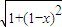 (0≤x≤1)的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC点P是边BC上的一动点,设CP=x,则AP+PF=f(x),请你参考这些信息,推知函数g(x)=4f(x)-9的零点的个数是 .
(0≤x≤1)的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC点P是边BC上的一动点,设CP=x,则AP+PF=f(x),请你参考这些信息,推知函数g(x)=4f(x)-9的零点的个数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com