(本小题满分12分)
试讨论函数
f(
x)=log
a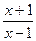
(
a>0且
a≠1)在(1,+∞)上的单调性,并予以证明.
解:设
u=
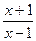
,任取
x2>
x1>1,则
u2-
u1=

=

=

.
∵
x1>1,
x2>1,∴
x1-1>0,
x2-1>0.
又∵
x1<
x2,

∴
x1-
x2<0.
∴

<0,即
u2<
u1.
当
a>1时,
y=log
ax是增函数,∴log
au2<log
au1,
即
f(
x2)<
f(
x1);
当0<
a<1时,
y=log
ax是减函数,∴log
au2>log
au1,
即
f(
x2)>
f(
x1).
综上可知,当
a>1时,
f(
x)=log
a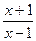
在(1,+∞)上为减函数;当0<
a<1时,
f(
x)=log
a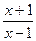
在(1,+∞)上为增函数.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:单选题
设

,则a, b,c的大小关系是( )
| A.a>c>b | B.a>b>c | C.c>a>b | D.b>c>a |
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
设f(x)=

若f(f (1))=1,则a=________.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分14分)
已知函数

为R上的奇函数
(1)求

的值
(2)求函数的值域
(3)判断函数的单调区间并证明
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知函数

则

_____________________
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
在1,-2,
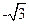
,0, π五个数中最小的数是
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
函数

的定义域为_________
查看答案和解析>>

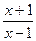 (a>0且a≠1)在(1,+∞)上的单调性,并予以证明.
(a>0且a≠1)在(1,+∞)上的单调性,并予以证明.