
分析 运用向量的数量积的定义:$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cos<$\overrightarrow{a}$,$\overrightarrow{b}$>,可得(1),(3),(4)错误,(2)正确.
解答 解:对于(1),$\overrightarrow{a}$•$\overrightarrow{b}$>0?cos<$\overrightarrow{a}$,$\overrightarrow{b}$>>0?<$\overrightarrow{a}$,$\overrightarrow{b}$>∈[0,$\frac{π}{2}$),
故(1)错误;
对于(2),(2)$\overrightarrow{a}$•$\overrightarrow{b}$=0?$\overrightarrow{a}$⊥$\overrightarrow{b}$?<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{2}$.
故(2)正确;
对于(3),$\overrightarrow{a}$•$\overrightarrow{b}$<0?cos<$\overrightarrow{a}$,$\overrightarrow{b}$><0?<$\overrightarrow{a}$,$\overrightarrow{b}$>∈($\frac{π}{2}$,π],
故(3)错误;
对于(4),|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$|?cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=1?<$\overrightarrow{a}$,$\overrightarrow{b}$>=0.
故(4)错误.
故答案为:1个.
点评 本题考查向量的数量积的定义和性质,考查向量的共线和垂直的条件,以及向量的夹角问题,属于基础题和易错题.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
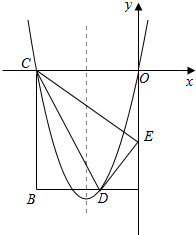 如图,在矩形ABCD中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
如图,在矩形ABCD中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
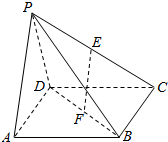 在四棱锥P-ABCD中,底面ABCD是正方形,AP⊥PD,侧面PAD⊥底面ABCD,点E、F分别为PC、BD的中点.
在四棱锥P-ABCD中,底面ABCD是正方形,AP⊥PD,侧面PAD⊥底面ABCD,点E、F分别为PC、BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com