
【题目】在![]() 中,内角A,B,C的对边分别是a,b,c,且a2+b2+
中,内角A,B,C的对边分别是a,b,c,且a2+b2+![]() ab=c2.
ab=c2.
(1)求C;
(2)设cos Acos B=![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)1或4.
;(2)1或4.
【解析】(1)因为a2+b2+![]() ab=c2,
ab=c2,
所以由余弦定理有cos C=![]() ,
,
故![]() .
.
(2)由题意得![]() =
=![]() ,
,
因此(tan αsin Acos A)(tan αsin Bcos B)=![]() ,
,
即tan2αsin Asin Btan α(sin Acos B+cos Asin B)+cos Acos B=![]() ,
,
即tan2αsin Asin Btan αsin(A+B)+cos Acos B=![]() ①.
①.
因为![]() ,
,
所以A+B=![]() ,
,
所以sin(A+B)=![]() .
.
因为cos(A+B)=cos Acos Bsin Asin B,即![]() -sin Asin B=
-sin Asin B=![]() ,
,
则sin Asin B=![]() .
.
代入①得tan2α5tan α+4=0,解得tan α=1或tan α=4.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2﹣3x,则函数g(x)=f(x)﹣x+3的零点的集合为( )
A.{1,3}
B.{﹣3,﹣1,1,3}
C.{2﹣ ![]() ,1,3}
,1,3}
D.{﹣2﹣ ![]() ,1,3}
,1,3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 是定义在(﹣1,1)上的奇函数,且f(
是定义在(﹣1,1)上的奇函数,且f( ![]() )=
)= ![]() ,则不等式f(t﹣1)+f(t)<0的解集为( )
,则不等式f(t﹣1)+f(t)<0的解集为( )
A.(0,1)
B.(0, ![]() ]
]
C.(0, ![]() )
)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着国民生活水平的提高,利用长假旅游的人越来越多.某公司统计了2012到2016年五年间本公司职员每年春节期间外出旅游的家庭数,具体统计数据如下表所示:

(Ⅰ)从这5年中随机抽取两年,求外出旅游的家庭数至少有1年多于20个的概率;
(Ⅱ)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程![]() ,判断它们之间是正相关还是负相关;并根据所求出的直线方程估计该公司2019年春节期间外出旅游的家庭数.
,判断它们之间是正相关还是负相关;并根据所求出的直线方程估计该公司2019年春节期间外出旅游的家庭数.
参考公式: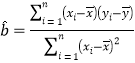 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() ,试估计该校学生每周平均体育运动时间超过4小时的概率.
,试估计该校学生每周平均体育运动时间超过4小时的概率.
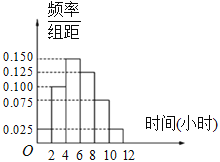
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时.请完成每周平均体育运动时间与性别的列联表,并判断能否在犯错误的概率不超过0.05的前提下认为该校学生的每周平均体育运动时间与性别有关?
男生 | 女生 | 合计 | |
每周平均体育运动时间不超过4小时 | |||
每周平均体育运动时间超过4小时 | |||
合计 | 300 |
附:![]() ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位建造一间地面面积为12m2的背面靠墙的矩形小房子,由于地理位置的限制,房子侧面的长度x不得超过am.房屋正面的造价为400元/m2 , 房屋侧面的造价为150元/m2 , 屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用.当侧面的长度为多少时,总造价最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg).其频率分布直方图如下:
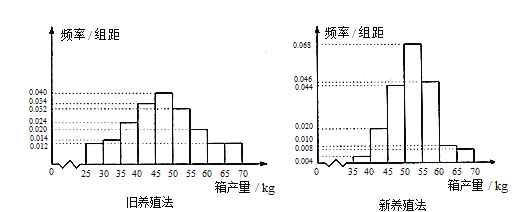
(1)设两种养殖方法的箱产量相互独立,记A表示事件:“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).
附: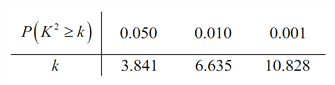 ,
, 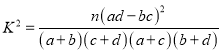
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com