
| ���� | 2��1�� | 2��2�� | 2��3�� | 2��4�� | 2��5�� |
| �²�x����C�� | 10 | 11 | 13 | 12 | 8 |
| ��ѿ��x���ţ� | 23 | 25 | 30 | 26 | 16 |
���� �����������оٳ���5��������ѡȡ2�����ݹ���10�������ÿ��������ǿ��ܳ��ֵģ������������¼������Ļ����¼���6�֣����ݵȿ����¼��ĸ������������
���������������ݣ�������x��y��ƽ�������������������ݵ��������ĵ㣬������С���˷�������Իع鷽�̵�ϵ����д�����Իع鷽�̲�����Ԥ����
��� �⣺������鵽�����ڵ���������Ϊ�¼�A����5��������ѡȡ2����
�ݹ���10���������1��2����1��3����1��4����1��5����2��3��
��2��4����2��5����3��4����3��5����4��5��������3�֣�
��������Ϊ12�·ݵ���������ÿ��������ǿ��ܳ��ֵģ�
�¼�A�����Ļ����¼���6�֣�
��P��A��=$\frac{3}{5}$��
��ѡȡ��2������ǡ���Dz�����2�����ݵĸ�����$\frac{3}{5}$����6�֣�
���������ݣ����$\overline{x}$=12��$\overline{y}$=27������8�֣�
�ɹ�ʽ�����$\stackrel{��}{b}$=2.5��$\stackrel{��}{a}$=-3
��y����x�����Իع鷽��Ϊ$\stackrel{��}{y}$=2.5x-3������10�֣�
�ɴ˿���Ԥ�����²�Ϊ20������ӷ�ѿ��Ϊ47�ţ�����12�֣�
���� ���⿼��ȿ����¼��ĸ��ʣ��������Իع鷽�̵���������С���˷�������ع�����ij���Ӧ�ã���һ���ۺ���Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | ������������ | δ������������ | �ϼ� |
| ������ҵ��Ա | 40 | 60 | 100 |
| �ǻ�����ҵ��Ա | 60 | 240 | 300 |
| �ϼ� | 100 | 300 | 400 |
| P��K2��k�� | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 0.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
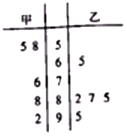 ijУ��ٰ조�������������һ��1����ļס�������ͬѧ�ڱ���μӣ������������ѡ�β��ԣ�����ͬ�IJ��������£�����5�β��Եijɼ�����λ���֣��ľ�Ҷͼ��ͼ��ʾ��
ijУ��ٰ조�������������һ��1����ļס�������ͬѧ�ڱ���μӣ������������ѡ�β��ԣ�����ͬ�IJ��������£�����5�β��Եijɼ�����λ���֣��ľ�Ҷͼ��ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1��m��$\frac{4}{5}$ | B�� | m��-1��m��1 | C�� | m=-1��m��1 | D�� | m=-1��0��m��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������� | B�� | ��Ҫ���� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com