
【题目】已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2﹣x;
(1)求函数f(x)的解析式;
(2)求不等式f(x)<0的解集.
【答案】(1),f(x)=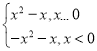 ,(2){x|x<﹣1或0<x<1}
,(2){x|x<﹣1或0<x<1}
【解析】
(1)设x<0,则﹣x>0,由当x≥0时,f(x)=x2﹣x,将﹣x>0代入解析式,由奇偶性即可求解.
(2)由(1)分段解不等式,再取并集即可.
(1)设x<0,则﹣x>0,∵当x≥0时,f(x)=x2﹣x,
∴f(﹣x)=x2+x,
∵f(x)是定义在R上的奇函数,
∴f(x)=﹣f(﹣x)=﹣x2﹣x,
∴当x<0时,f(x)=﹣x2﹣x,
综上所述,f(x)=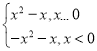 ;
;
(2)当x≥0时,f(x)=x2﹣x<0,∴0<x<1;
当x<0时,f(x)=﹣x2﹣x<0,∴x<﹣1或x>0,∴x<﹣1,
综上所述,不等式f(x)<0的解集为{x|x<﹣1或0<x<1}.


科目:高中数学 来源: 题型:
【题目】某校有![]() 、
、![]() 、
、![]() 、
、![]() 四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖,在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下.
四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖,在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下.
甲说:“![]() 、
、![]() 同时获奖.”
同时获奖.”
乙说:“![]() 、
、![]() 不可能同时获奖.”
不可能同时获奖.”
丙说:“![]() 获奖.”
获奖.”
丁说:“![]() 、
、![]() 至少一件获奖”
至少一件获奖”
如果以上四位同学中有且只有两位同学的预测是正确的,则获奖的作品是( )
A. 作品![]() 与作品
与作品![]() B. 作品
B. 作品![]() 与作品
与作品![]() C. 作品
C. 作品![]() 与作品
与作品![]() D. 作品
D. 作品![]() 与作品
与作品![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为4,动点E,F在棱
的棱长为4,动点E,F在棱![]() 上,动点P,Q分别在棱AD,CD上。若
上,动点P,Q分别在棱AD,CD上。若![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 大于零),则四面体PEFQ的体积
大于零),则四面体PEFQ的体积
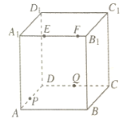
A.与![]() 都有关B.与m有关,与
都有关B.与m有关,与![]() 无关
无关
C.与p有关,与![]() 无关D.与π有关,与
无关D.与π有关,与![]() 无关
无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,g(x)=f(x)﹣3.
,g(x)=f(x)﹣3.
(1)判断并证明函数g(x)的奇偶性;
(2)判断并证明函数g(x)在(1,+∞)上的单调性;
(3)若f(m2﹣2m+7)≥f(2m2﹣4m+4)成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】蚌埠市某中学高三年级从甲(文)、乙(理)两个科组各选出![]() 名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是
名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是![]() ,乙组学生成绩的中位数是
,乙组学生成绩的中位数是![]() .
.
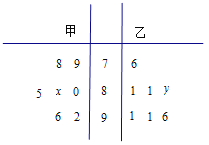
(1)求![]() 和
和![]() 的值;
的值;
(2)计算甲组![]() 位学生成绩的方差
位学生成绩的方差![]() ;
;
(3)从成绩在![]() 分以上的学生中随机抽取两名学生,求甲组至少有一名学生的概率.
分以上的学生中随机抽取两名学生,求甲组至少有一名学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点,点
的中点,点![]() 为上底面的中心,过
为上底面的中心,过![]() ,
,![]() ,
,![]() 三点的平面把正方体分为两部分,其中含
三点的平面把正方体分为两部分,其中含![]() 的部分为
的部分为![]() ,不含
,不含![]() 的部分为
的部分为![]() ,连结
,连结![]() 和
和![]() 的任一点
的任一点![]() ,设
,设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() 的最大值为
的最大值为

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com