
【题目】如图所示,一辆汽车从![]() 市出发沿海岸一条直公路以
市出发沿海岸一条直公路以![]() 的速度向东匀速行驶,汽车开动时,在
的速度向东匀速行驶,汽车开动时,在![]() 市南偏东方向距
市南偏东方向距![]() 市
市![]() 且与海岸距离为
且与海岸距离为![]() 的海上
的海上![]() 处有一快艇与汽车同时出发,要把一份稿件送给这辆汽车的司机.
处有一快艇与汽车同时出发,要把一份稿件送给这辆汽车的司机.

(1)快艇至少以多大的速度行驶才能把稿件送到司机手中?
(2)在(1)的条件下,求快艇以最小速度行驶时的行驶方向与![]() 所成的角.
所成的角.
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】设n 为不小于3的正整数,集合![]() ,对于集合
,对于集合![]() 中的任意元素
中的任意元素![]() ,
,![]() 记
记![]()
(Ⅰ)当![]() 时,若
时,若![]() ,请写出满足
,请写出满足![]() 的所有元素
的所有元素![]()
(Ⅱ)设![]() 且
且![]() ,求
,求![]() 的最大值和最小值;
的最大值和最小值;
(Ⅲ)设S是![]() 的子集,且满足:对于S中的任意两个不同元素
的子集,且满足:对于S中的任意两个不同元素![]() ,有
,有![]() 成立,求集合S中元素个数的最大值.
成立,求集合S中元素个数的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某住宅小区为了使居民有一个优雅、舒适的生活环境,计划建一个八边形的休闲小区,其主体造型的平面图是由两个相同的矩形ABCD和矩形EFGH构成的面积是200 m2的十字形区域,现计划在正方形MNPQ上建一花坛,造价为4 200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角上铺草坪,造价为80元/m2.
(1)设总造价为S元,AD的边长为x m,试建立S关于x的函数解析式;
(2)计划至少要投多少万元才能建造这个休闲小区?

查看答案和解析>>
科目:高中数学 来源: 题型:
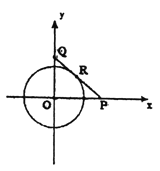
【题目】设有半径为![]() 的圆形村落,
的圆形村落, ![]() 两人同时从村落中心出发,
两人同时从村落中心出发, ![]() 向北直行,
向北直行, ![]() 先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与
先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与![]() 相遇.设
相遇.设![]() 两人速度一定,其速度比为
两人速度一定,其速度比为![]() ,问两人在何处相遇?
,问两人在何处相遇?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 上一点,经过点
上一点,经过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点(不同于点
两点(不同于点![]() ),直线
),直线![]() 、
、![]() 分别交直线
分别交直线![]() 于点
于点![]() 、
、![]() .
.
(1)求抛物线方程及其焦点坐标;
(2)求证:以![]() 为直径的圆恰好经过原点.
为直径的圆恰好经过原点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的侧面
的侧面![]() 是平行四边形,
是平行四边形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 分别是
分别是![]() 的中点.
的中点.

(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的二项式
的二项式![]() 的展开式的二项式系数之和为1024,常数项为180.
的展开式的二项式系数之和为1024,常数项为180.
(1)求![]() 和
和![]() 的值;
的值;
(2)求展开式中的无理项.(不需求项的表达式,指出无理项的序号即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com