
【题目】三棱锥P ABC中,PA⊥平面ABC,![]() Q是BC边上的一个动点,且直线PQ与面ABC所成角的最大值为
Q是BC边上的一个动点,且直线PQ与面ABC所成角的最大值为![]() 则该三棱锥外接球的表面积为( )
则该三棱锥外接球的表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
根据题意画出图形,结合图形找出△ABC的外接圆圆心与三棱锥P﹣ABC外接球的球心,
求出外接球的半径,再计算它的表面积.
三棱锥P﹣ABC中,PA⊥平面ABC,直线PQ与平面ABC所成角为θ,
如图所示;则sinθ=![]() =
=![]() ,且sinθ的最大值是
,且sinθ的最大值是![]() ,
,
∴(PQ)min=2![]() ,∴AQ的最小值是
,∴AQ的最小值是![]() ,即A到BC的距离为
,即A到BC的距离为![]() ,
,
∴AQ⊥BC,∵AB=2![]() ,在Rt△ABQ中可得
,在Rt△ABQ中可得![]() ,即可得BC=6;
,即可得BC=6;
取△ABC的外接圆圆心为O′,作OO′∥PA,
∴![]() =2r,解得r=2
=2r,解得r=2![]() ;
;
∴O′A=2![]() ,
,
取H为PA的中点,∴OH=O′A=2![]() ,PH=
,PH=![]() ,
,
由勾股定理得OP=R=![]() =
=![]() ,
,
∴三棱锥P﹣ABC的外接球的表面积是
S=4πR2=4×![]() =57π.
=57π.
故答案为:C


科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣2x﹣3≤0,x∈R},B={x|(x﹣m+2)(x﹣m﹣2)≤0,x∈R,m∈R}.
(1)若A∩B={x|0≤x≤3},求实数m的值;
(2)若ARB,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
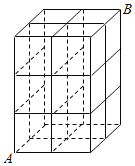
【题目】如图,某建筑工地搭建的脚手架局部类似于一个![]() 的长方体框架,一个建筑工人欲从
的长方体框架,一个建筑工人欲从![]() 处沿脚手架攀登至
处沿脚手架攀登至 ![]() 处,则其最近的行走路线中不连续向上攀登的概率为( )
处,则其最近的行走路线中不连续向上攀登的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P ABCD中,E是棱PC上一点,且2![]() ,底面ABCD是边长为2的正方形,△PAD为正三角形,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l,且平面PAD⊥平面ABCD.
,底面ABCD是边长为2的正方形,△PAD为正三角形,平面ABE与棱PD交于点F,平面PCD与平面PAB交于直线l,且平面PAD⊥平面ABCD.

(1)求证:l∥EF;
(2)求四棱锥P-ABEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的四棱锥S﹣ABCD中,SA⊥底面ABCD,∠DAB=∠ABC=90°,SA=AB=BC=a,AD=3a(a>0),E为线段BS上的一个动点. 
(1)证明:DE和SC不可能垂直;
(2)当点E为线段BS的三等分点(靠近B)时,求二面角S﹣CD﹣E的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com