练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．在等差数列{an}中a3+a11=40，则a4-a5+a6+a7+a8-a9+a10的值（　　）
    A．84B．72C．60D．48

    分析 由等差数列的通项公式求出a7=20，由此能求出a4-a5+a6+a7+a8-a9+a10的值．

    解答 解：∵在等差数列{an}中a3+a11=40，
    ∴a3+a11=2a7=40，解得a7=20，
    ∴a4-a5+a6+a7+a8-a9+a10=3a7=60．
    故选：C．

    点评 本题考查等差数列的若干项的代数和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．已知$\overrightarrow a$，$\overrightarrow b$是非零向量，且向量$\overrightarrow a$，$\overrightarrow b$的夹角为$\frac{π}{3}$，若向量$\overrightarrow p=\frac{\overrightarrow a}{|\overrightarrow a|}+\frac{\overrightarrow b}{|\overrightarrow b|}$，则$|\overrightarrow p|$=（　　）
    A．$2+\sqrt{3}$B．$\sqrt{2+\sqrt{3}}$C．3D．$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．设min{p，q}表示p，q两者中的较小者，若函数f（x）=min{3-x，log2x}，则f（x）的最大值为2，满足$f（x）＜\frac{1}{2}$的集合为{x|0＜x＜$\sqrt{2}$或x＞$\frac{5}{2}$}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

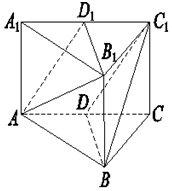    2．如图所示，在三棱柱ABC-A1B1C1中，点D为AC的中点，点D1是A1C1中点
    （1）求证：BC1∥平面AB1D1
    （2）求证：平面AB1D1∥平面C1BD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．如图，已知椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的离心率e=$\frac{1}{2}$，长轴长为4．
    （1）求椭圆C的方程；
    （2）设动直线l1：y=kx+m与椭圆C有且只有一个公共点P，过右焦点F作直线l2与直线l1交与点Q，且$\overrightarrow{PF}$•$\overrightarrow{FQ}$=0．求证：点Q在定直线上，并求出定直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

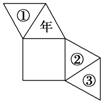    10．某人用如图所示的纸片，沿折痕折后粘成一个四棱锥形的“走马灯”，正方形做灯底，且有一个三角形面上写上了“年”字，当灯旋转时，正好看到“新年快乐”的字样，则在①、②、③处应依次写上（　　）
    A．快、新、乐B．乐、新、快C．新、乐、快D．乐、快、新

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知函数f（x）（x∈R）是奇函数，且当x＞0时，f（x）=2x-1．
    （1）求函数f（x）的解析式；     
    （2）求f（f（-2））的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知f（x）=x+1，g（x）=-2x，$F（x）=\left\{\begin{array}{l}f（x），f（x）＜g（x）\\ g（x），f（x）≥g（x）\end{array}\right.$，则F（x）的最值是（　　）
    A．有最大值为$\frac{2}{3}$，无最小值B．有最大值为$-\frac{1}{3}$，无最小值
    C．有最小值为$-\frac{1}{3}$，无最大值D．有最小值为$\frac{2}{3}$，无最大值

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．下列是函数y=-（x-3）|x|的递增区间是（　　）
    A．（-∞，3）B．（0，3）C．$（{0，\frac{3}{2}}）$D．$（{\frac{3}{2}，3}）$

    查看答案和解析>>

    同步练习册答案