
分析 根据向量的坐标运算和向量的垂直的条件以及向量的模,即可求出.
解答 解:∵$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(1,1),
∴$\overrightarrow{c}$=$λ\overrightarrow{a}+μ\overrightarrow{b}$(λ+μ,μ),
∵$\overrightarrow{c}⊥\overrightarrow{b}$,
∴λ+μ+μ=0,即λ=-2μ,①,
∵|$\overrightarrow{c}$|=$\sqrt{2}$,
∴(λ+μ)2+μ2=4,②,
由①②构成方程组,解得$\left\{\begin{array}{l}{λ=-2\sqrt{2}}\\{μ=\sqrt{2}}\end{array}\right.$,或$\left\{\begin{array}{l}{λ=2\sqrt{2}}\\{μ=-\sqrt{2}}\end{array}\right.$.
点评 本题考查平面向量数量积的运算,考查运算求解能力,注意解题方法的积累,属于基础题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
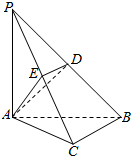 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC.
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com