
【题目】已知函数f (x)=Asin(ωx+φ),(0<φ<π)的图象如图所示,若f (x0)=3,x0∈( ![]() ,
, ![]() ),则sinx0的值为( )
),则sinx0的值为( ) 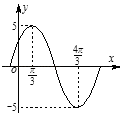
A.![]()
B.![]()
C.![]()
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知直三棱柱ABC﹣A1B1C1的底面为正三角形,E,F分别是A1C1 , B1C1上的点,且满足A1E=EC1 , B1F=3FC1 . 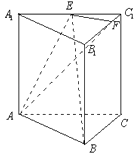
(1)求证:平面AEF⊥平面BB1C1C;
(2)设直三棱柱ABC﹣A1B1C1的棱长均相等,求二面角C1﹣AE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔船在航行中不幸遇险,发出呼叫信号,我海军舰艇在![]() 处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为
处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为![]() ,距离为15海里的
,距离为15海里的![]() 处,并测得渔船正沿方位角为
处,并测得渔船正沿方位角为![]() 的方向,以15海里/小时的速度向小岛
的方向,以15海里/小时的速度向小岛![]() 靠拢,我海军舰艇立即以
靠拢,我海军舰艇立即以![]() 海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.
海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店对新引进的商品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
定价 | 9 | 9.2 | 9.4 | 9.6 | 9.8 | 10 |
销量 | 100 | 94 | 93 | 90 | 85 | 78 |
(1)求回归直线方程![]() ;
;
(2)假设今后销售依然服从(Ⅰ)中的关系,且该商品金价为每件5元,为获得最大利润,商店应该如何定价?(利润=销售收入-成本)
参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种水果的单个质量在500g以上视为特等品.随机抽取1000个该水果,结果有50个特等品.将这50个水果的质量数据分组,得到下边的频率分布表.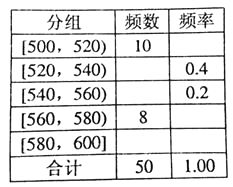
(1)估计该水果的质量不少于560g的概率;
(2)若在某批水果的检测中,发现有15个特等品,据此估计该批水果中没有达到特等品的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个 ![]() 列联表;
列联表;
(2)判断性别与休闲方式是否有关系.
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:

(1)求分数![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的中位数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种产品,每年需投入固定成本0.5万元,此外每生产100件这样的产品,还需增加投入0.25万元,经市场调查知这种产品年需求量为500件,产品销售数量为 ![]() 件时,销售所得的收入为
件时,销售所得的收入为 ![]() 万元.
万元.
(1)该公司这种产品的年生产量为 ![]() 件,生产并销售这种产品所得到的利润关于当年产量
件,生产并销售这种产品所得到的利润关于当年产量 ![]() 的函数为
的函数为 ![]() ,求
,求 ![]() ;
;
(2)当该公司的年产量为多少件时,当年所获得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,已知点P的直角坐标为(1,2),点M的极坐标为 ![]() ,若直线l过点P,且倾斜角为
,若直线l过点P,且倾斜角为 ![]() ,圆C以M为圆心,3为半径.
,圆C以M为圆心,3为半径.
(Ⅰ)求直线l的参数方程和圆C的极坐标方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA||PB|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com