练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设三棱锥的3条侧棱两两垂直，其长度分别为2、4、4，则其外接球的表面积为（ ）
    A．48π
    B．36π
    C．32π
    D．12π
    【答案】分析：由题意三棱锥扩展为长方体，它们的外接球相同，长方体的对角线的长度就是外接球的直径，求出半径，即可求解球的表面积．
    解答：解：因为三棱锥的3条侧棱两两垂直，其长度分别为2、4、4，
    所以三棱锥扩展为长方体，它们的外接球相同，长方体的对角线的长度就是外接球的直径，
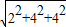
    所以球的直径为：=6，
    外接球的半径为：3．
    外接球的表面积为：4×32π=36π．
    故选B．
    点评：本题考查球的内接多面体与球的体积的求法，考查空间想象能力，计算能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设三棱锥的3条侧棱两两垂直，其长度分别为2、4、4，则其外接球的表面积为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    设三棱锥的3条侧棱两两垂直，其长度分别为2、4、4，则其外接球的表面积为


    1. A.
      48π
    2. B.
      36π
    3. C.
      32π
    4. D.
      12π

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设三棱锥的3条侧棱两两垂直，其长度分别为2、4、4，则其外接球的表面积为(　　)

    (A)48π  (B)36π  (C)32π  (D)12π

    查看答案和解析>>

    科目：高中数学 来源：甘肃省月考题 题型：单选题

    设三棱锥的3条侧棱两两垂直，其长度分别为2、4、4，则其外接球的表面积为
    [     ]
    A.48π
    B.36π
    C.32π
    D.12π

    查看答案和解析>>

    同步练习册答案