
【题目】已知f(x)是R上的奇函数,当x>0时,解析式为f(x)=![]() .
.
(1)求f(x)在R上的解析式;
(2)用定义证明f(x)在(0,+∞)上为减函数.
【答案】(1) f(x)=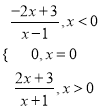 (2)见解析
(2)见解析
【解析】试题分析:(1)分别求出当x<0和x=0时的解析式,写成分段函数的形式;(2)设x1,x2∈(0,+∞),且x1<x2,通过作差证明f(x1)>f(x2)即可。
试题解析:(1)设x<0,则-x>0,
∴f(-x)=![]() .
.
又∵f(x)是R上的奇函数,
∴f(-x)=-f(x)=![]() ,
,
∴f(x)=![]() .
.
又∵奇函数在x=0时有意义,
∴f(0)=0,
∴函数的解析式为f(x)=
(2)证明:设x1,x2∈(0,+∞),且x1<x2,
则f(x1)-f(x2)=![]() -
-![]() =
=
![]()
=![]() .
.
∵x1,x2∈(0,+∞),x1<x2,
∴x1+1>0,x2+1>0,x2-x1>0,
∴f(x1)-f(x2)>0,
∴f(x1)>f(x2),
∴函数f(x)在(0,+∞)上为减函数.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
:![]() .
.

⑴若圆![]() 的半径为2,圆
的半径为2,圆![]() 与
与![]() 轴相切且与圆
轴相切且与圆![]() 外切,求圆
外切,求圆![]() 的标准方程;
的标准方程;
⑵若过原点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣1﹣alnx.
(Ⅰ)若 f(x)≥0,求a的值;
(Ⅱ)设m为整数,且对于任意正整数n,(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<m,求m的最小值.
)<m,求m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(ax-bx),(a>1>b>0).
(1)求f(x)的定义域;
(2)若f(x)在(1,+∞)上递增且恒取正值,求a,b满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com