Question

【题目】已知矩形ABCD，AB=1，BC= ． 将△ABD沿矩形的对角线BD所在的直线进行翻折，在翻折过程中（　　）
A.存在某个位置，使得直线AC与直线BD垂直
B.存在某个位置，使得直线AB与直线CD垂直
C.存在某个位置，使得直线AD与直线BC垂直
D.对任意位置，三对直线“AC与BD”，“AB与CD”，“AD与BC”均不垂直

Answer 1

【答案】B
【解析】解：如图，AE⊥BD，CF⊥BD，依题意，AB=1，BC= ， AE=CF= ， BE=EF=FD= ，
A，若存在某个位置，使得直线AC与直线BD垂直，则∵BD⊥AE，∴BD⊥平面AEC，从而BD⊥EC，这与已知矛盾，排除A；
B，若存在某个位置，使得直线AB与直线CD垂直，则CD⊥平面ABC，平面ABC⊥平面BCD
取BC中点M，连接ME，则ME⊥BD，∴∠AEM就是二面角A﹣BD﹣C的平面角，此角显然存在，即当A在底面上的射影位于BC的中点时，直线AB与直线CD垂直，故B正确；
C，若存在某个位置，使得直线AD与直线BC垂直，则BC⊥平面ACD，从而平面ACD⊥平面BCD，即A在底面BCD上的射影应位于线段CD上，这是不可能的，排除C
D，由上所述，可排除D
故选 B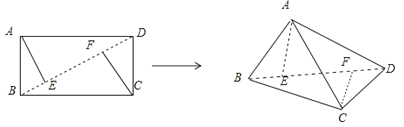

【考点精析】掌握空间中直线与直线之间的位置关系是解答本题的根本，需要知道相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点．