
| A. | ($\sqrt{5}$,$\sqrt{10}$] | B. | (1,$\sqrt{10}$] | C. | (1,$\sqrt{5}$] | D. | [$\sqrt{5}$,+∞) |
分析 可设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)与直线y=2x有交点,应有$\frac{b}{a}$>2,再联立直线y=3x,由于没有交点,则$\frac{b}{a}$≤3,可得e的范围.
解答 解:设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的渐近线方程为y=±$\frac{b}{a}$x,
双曲线与直线y=2x有交点,
则有$\frac{b}{a}$>2,
又双曲线与直线y=3x没有公共点,
则有$\frac{b}{a}$≤3,
即有2<$\frac{b}{a}$≤3,
即有2<$\frac{\sqrt{{c}^{2}-{a}^{2}}}{a}$≤3,即2<$\sqrt{{e}^{2}-1}$≤3,
解得$\sqrt{5}$<e≤$\sqrt{10}$.
故选A.
点评 本题考查了双曲线的渐近线和离心率,直线与双曲线相交等问题,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | y=g(x)的图象关于点(-$\frac{π}{3}$,0)中心对称 | B. | y=g(x)的图象关于x=-$\frac{π}{6}$轴对称 | ||
| C. | y=g(x)在区间[-$\frac{5π}{12}$,-$\frac{π}{6}$]单调递增 | D. | y=g(x)在[-$\frac{π}{6}$,$\frac{π}{3}$]单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| API | [0.50] | (0,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 非重度污染 | 重度污染 | 合计 | |
| 供暖季 | |||
| 非供暖季 | |||
| 合计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
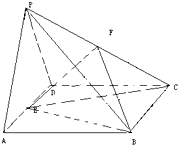 如图,△PAD为边长为2的等边三角形,ABCD为菱形,∠DAB=60°,E为AD的中点,平面PAD⊥平面ABCD,F为棱PC上一点,
如图,△PAD为边长为2的等边三角形,ABCD为菱形,∠DAB=60°,E为AD的中点,平面PAD⊥平面ABCD,F为棱PC上一点,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com