
分析 求出原函数的导函数.
(1)对a分类可得f'(x)、f(x)的变化情况表,利用表格可得函数f(x)的单调区间;
(2)求出f(1)=$-\frac{1}{2}-a$,可得a>0时,f(1)<0,此时f(x)≥0对定义域内的任意x不是恒成立;a≤0时,求出函数f(x)在区间(0,+∞)的极小值,也是最小值,由最小值大于等于0求得a的取值范围.
解答 解:$f'(x)=\frac{a}{x}+x-({1+a})=\frac{{{x^2}-({1+a})x+a}}{x}=\frac{{({x-1})({x-a})}}{x}$,
(1)①当0<a<1时,f'(x)、f(x)的变化情况如下表:
| x | (0,a) | a | (a,1) | 1 | (1,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
| x | (0,1) | 1 | (1,a) | a | (a,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
点评 本题考查利用导数研究函数的单调性,考查了利用导数求函数在闭区间上的最值,体现了分类讨论的数学思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
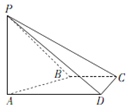 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,AD=2BC=2CD.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,AD=2BC=2CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 10 | C. | 2$\sqrt{6}$ | D. | 4$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2kπ}{3}-\frac{π}{9}$,$\frac{2kπ}{3}+\frac{2π}{9}$),k∈Z | B. | ($\frac{2kπ}{3}$-$\frac{4π}{9}$,$\frac{2kπ}{3}$-$\frac{π}{9}$),k∈Z | ||
| C. | ($\frac{2kπ}{3}$+$\frac{π}{18}$,$\frac{2kπ}{3}$+$\frac{7π}{18}$),k∈Z | D. | ($\frac{2kπ}{3}$-$\frac{7π}{18}$,$\frac{2kπ}{3}-\frac{π}{18}$),k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 心理健康教育老师对某班50个学生进行了心里健康测评,测评成绩满分为100分.成绩出来后,老师对每个成绩段的人数进行了统计,并得到如图4所示的频率分布直方图.
心理健康教育老师对某班50个学生进行了心里健康测评,测评成绩满分为100分.成绩出来后,老师对每个成绩段的人数进行了统计,并得到如图4所示的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com