
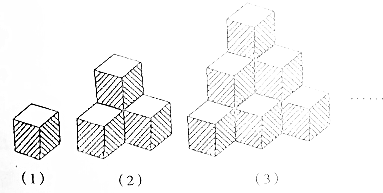
 如图是由一些小正方体摞成的,第(1)堆有1个,第(2)堆有4个,第(3)堆有10个…,则第n堆有$\frac{n(n+1)(n+2)}{6}$小正方体.
如图是由一些小正方体摞成的,第(1)堆有1个,第(2)堆有4个,第(3)堆有10个…,则第n堆有$\frac{n(n+1)(n+2)}{6}$小正方体. 科目:高中数学 来源: 题型:选择题
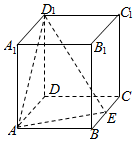 如图,正方体ABCD-A1B1C1D1中,E是棱BC的中点,F是侧面BCC1B1上的动点,且A1F∥平面AD1E,则直线A1F与平面BCC1B1所成的角的正切值t构成的集合是( )
如图,正方体ABCD-A1B1C1D1中,E是棱BC的中点,F是侧面BCC1B1上的动点,且A1F∥平面AD1E,则直线A1F与平面BCC1B1所成的角的正切值t构成的集合是( )| A. | {t|${\frac{{2\sqrt{5}}}{5}$≤t≤$\frac{{2\sqrt{3}}}{3}}\right.}$} | B. | {t|{2≤t≤2$\sqrt{3}}$} | C. | {t|${\frac{{2\sqrt{5}}}{5}$≤t≤2$\sqrt{3}$} | D. | {{t|{2≤t≤2$\sqrt{2}}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨q | B. | p∧q | C. | p∨q | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=$\sqrt{3}$,AB=$\sqrt{2}$,AC=2,A1C1=1,$\frac{BD}{DC}$=$\frac{1}{2}$.
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=$\sqrt{3}$,AB=$\sqrt{2}$,AC=2,A1C1=1,$\frac{BD}{DC}$=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
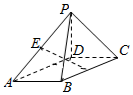 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PD⊥底面ABCD,PD=1,PB=PC=BC=$\sqrt{2}$,点E,F分别是PA,BC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PD⊥底面ABCD,PD=1,PB=PC=BC=$\sqrt{2}$,点E,F分别是PA,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
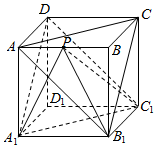
| A. | 平面ACB1∥平面A1C1D,且两平面的距离为$\frac{{\sqrt{3}}}{3}$ | |
| B. | 点P在线段AB上运动,则四面体PA1B1C1的体积不变 | |
| C. | 与所有12条棱都相切的球的体积为$\frac{{\sqrt{2}}}{3}$π | |
| D. | M是正方体的内切球的球面上任意一点,N是△AB1C外接圆的圆周上任意一点,则|MN|的最小值是$\frac{{\sqrt{3}-\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,对大于等于2的自然数m的n次幂进行如图方式的“分裂”,如23的“分裂”中最大的数是5,34的“分裂”中最大的数是29,那么20163的“分裂”中最大的数是20162+2015.(写出算式即可)
如图,对大于等于2的自然数m的n次幂进行如图方式的“分裂”,如23的“分裂”中最大的数是5,34的“分裂”中最大的数是29,那么20163的“分裂”中最大的数是20162+2015.(写出算式即可)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com