
 ������д�������е�һ��ͨ�ʽ��
������д�������е�һ��ͨ�ʽ�� ��c=-1��������һ������bn=Asin����n+�գ�+B��ͨ�ʽ������A��B���ء��վ�Ϊʵ����A��0���أ�0��|��|��
��c=-1��������һ������bn=Asin����n+�գ�+B��ͨ�ʽ������A��B���ء��վ�Ϊʵ����A��0���أ�0��|��|��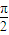 ��������е�һ��ͨ�ʽbn��
��������е�һ��ͨ�ʽbn�� ���æ�=
���æ�=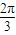 ������bn=Asin��
������bn=Asin�� n+�գ�+B����b1=2��b2=
n+�գ�+B����b1=2��b2= ��b3=-1��������ʽ�����ɵó����ۣ�
��b3=-1��������ʽ�����ɵó����ۣ�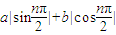 �ȣ���3�֣�
�ȣ���3�֣� ����5�֣�
����5�֣�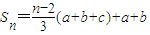 ����7�֣�
����7�֣� ��k��N������9�֣�
��k��N������9�֣� ���æ�=
���æ�=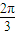 ����10�֣�
����10�֣�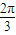 n+�գ�+B��
n+�գ�+B�� ��b3=-1��������ʽ��
��b3=-1��������ʽ��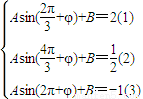 ��12�֣�
��12�֣�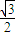 ���ٴ��루1����չ��ʽ���ɵ�-
���ٴ��루1����չ��ʽ���ɵ�- ��+B=
��+B= ���루3��������B=
���루3��������B= ����13�֣�
����13�֣� ������tan��=-
������tan��=-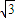
 �����Ԧ�=-
�����Ԧ�=- ����14�֣�
����14�֣� ����15�֣�
����15�֣� sin��
sin��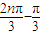 ��+
��+ ��16�֣�
��16�֣�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 4x+2 |
| x+3 |
| ax+b |
| cx+d |
| an-x1 |
| an-x2 |
| lim |
| n���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
| 1 |
| 2 |
| �� |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
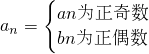 ������д�������е�һ��ͨ�ʽ��
������д�������е�һ��ͨ�ʽ�� ��c=-1��������һ������bn=Asin����n+�գ�+B��ͨ�ʽ������A��B���ء��վ�Ϊʵ����A��0���أ�0��|��|��
��c=-1��������һ������bn=Asin����n+�գ�+B��ͨ�ʽ������A��B���ء��վ�Ϊʵ����A��0���أ�0��|��|��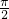 ��������е�һ��ͨ�ʽbn��
��������е�һ��ͨ�ʽbn���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
| 4x+2 |
| x+3 |
| ax+b |
| cx+d |
| an-x1 |
| an-x2 |
| lim |
| n���� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com