
【题目】设![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,将数列
,将数列![]() 的前100项从大到小排列得到数列
的前100项从大到小排列得到数列![]() ,若
,若![]() ,则k的值为______;
,则k的值为______;
【答案】![]()
【解析】
根据递推公式利用数学归纳法分析出![]() 与
与![]() 的关系,然后考虑将
的关系,然后考虑将![]() 的前
的前![]() 项按要求排列,再根据项的序号计算出满足的
项按要求排列,再根据项的序号计算出满足的![]() 值即可.
值即可.
由已知,a1=a,0<a<1;并且函数y=ax单调递减;
∵![]()
∴1>a2>a1
∴![]() ,
,
∴a2>a3>a1
∵![]() ,且
,且![]()
∴a2>a4>a3>a1
……
当![]() 为奇数时,用数学归纳法证明
为奇数时,用数学归纳法证明![]() ,
,
当![]() 时,
时,![]() 成立,
成立,
设![]() 时,
时,![]() ,
,
当![]() 时,因为
时,因为![]() ,结合
,结合![]() 的单调性,
的单调性,
所以![]() ,所以
,所以![]() 即
即![]() ,所以
,所以![]() 时成立,
时成立,
所以![]() 为奇数时,
为奇数时,![]() ;
;
当![]() 为偶数时,用数学归纳法证明
为偶数时,用数学归纳法证明![]() ,
,
当![]() 时,
时,![]() 成立,设
成立,设![]() 时,
时,![]() ,
,
当![]() 时,因为
时,因为![]() ,结合
,结合![]() 的单调性,
的单调性,
所以![]() ,所以
,所以![]() 即
即![]() ,所以
,所以![]() 时成立,
时成立,
所以![]() 为偶数时,
为偶数时,![]() ;
;
用数学归纳法证明:任意偶数项大于相邻的奇数项即证:当![]() 为奇数,
为奇数,![]() ,
,
当![]() 时,
时,![]() 符合,设
符合,设![]() 时,
时,![]() ,
,
当![]() 时,因为
时,因为![]() ,结合
,结合![]() 的单调性,
的单调性,
所以![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() 时成立,
时成立,
所以当![]() 为奇数时,
为奇数时,![]() ,
,
据此可知:![]() ,
,
当![]() 时,若
时,若![]() ,则有
,则有![]() ,此时
,此时![]() 无解;
无解;
当![]() 时,此时
时,此时![]() 的下标成首项为
的下标成首项为![]() 公差为
公差为![]() 的等差数列,通项即为
的等差数列,通项即为![]() ,
,
若![]() ,所以
,所以![]() ,所以
,所以![]() .
.
故答案为:![]() .
.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响某校随机抽取200名学生,对学习成绩和学案使用程度进行了调查,统计数据如下表所示:
善于使用学案 | 不善于使用学案 | 合计 | |
学习成绩优秀 | 40 | ||
学习成绩一般 | 30 | ||
合计 | 200 |
已知随机抽查这200名学生中的一名学生,抽到善于使用学案的学生概率是0.6.
参考公式:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(I)完成![]() 列联表(不用写计算过程);
列联表(不用写计算过程);
(Ⅱ)试运用独立性检验的思想方法分析有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前共享单车基本覆盖饶城市区,根据统计,市区所有人骑行过共享单车的人数已占![]() ,骑行过共享单车的人数中,有
,骑行过共享单车的人数中,有![]() 是学生(含大中专、高职及中学生),若市区人口按40万计算,学生人数约为9.6万.
是学生(含大中专、高职及中学生),若市区人口按40万计算,学生人数约为9.6万.
(1)任选出一名学生,求他(她)骑行过共享单车的概率;
(2)随着单车投放数量增加,乱停乱放成为城市管理的问题,如表是本市某组织累计投放单车数量![]() 与乱停乱放单车数量
与乱停乱放单车数量![]() 之间关系图表:
之间关系图表:
累计投放单车数量 | 100000 | 120000 | 150000 | 200000 | 230000 |
乱停乱放单车数量 | 1400 | 1700 | 2300 | 3000 | 3600 |
计算![]() 关于
关于![]() 的线性回归方程(其中
的线性回归方程(其中![]() 精确到
精确到![]() ,
,![]() 值保留三位有效数字),并预测当
值保留三位有效数字),并预测当![]() 时,单车乱停乱放的数量;
时,单车乱停乱放的数量;
(3)已知信州区、广丰区、上饶县、经开区四区中,其中有两个区的单车乱停乱放数量超过标准,在“大美上饶”活动中,检查组随机抽取两个区调查单车乱停乱放数量,![]() 表示“单车乱停乱放数量超过标准的区的个数”,求
表示“单车乱停乱放数量超过标准的区的个数”,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式和数据:回归直线方程![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为
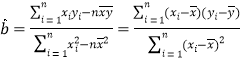 ,
,![]() ,
,
![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一布袋中装有![]() 个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是( )
个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是( )
A. 若![]() ,则乙有必赢的策略B. 若
,则乙有必赢的策略B. 若![]() ,则甲有必赢的策略
,则甲有必赢的策略
C. 若![]() ,则甲有必赢的策略D. 若
,则甲有必赢的策略D. 若![]() ,则乙有必赢的策略
,则乙有必赢的策略
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区抽取50户居民进行月用电量调查,发现其用电量都在50到350度之间,将用电量的数据绘制成频率分布直方图如下.

(1)求频率分布直方图中![]() 的值并估计这50户用户的平均用电量;
的值并估计这50户用户的平均用电量;
(2)若将用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为低用电家庭,用电量在区间
类用户,标记为低用电家庭,用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
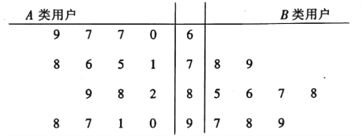
①从![]() 类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
②若打分超过85分视为满意,没超过85分视为不满意,请填写下面列联表,并根据列联表判断是否有![]() 的把握认为“满意度与用电量高低有关”?
的把握认为“满意度与用电量高低有关”?
满意 | 不满意 | 合计 | |
| |||
| |||
合计 |
附表及公式:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
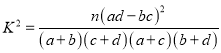 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点为极点,以
为参数),以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)若![]() 与曲线
与曲线![]() 相切,且
相切,且![]() 与坐标轴交于
与坐标轴交于![]() 两点,求以
两点,求以![]() 为直径的圆的极坐标方程.
为直径的圆的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<![]() )的图象如图所示.
)的图象如图所示.
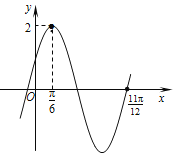
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调增区间;
(3)若x∈[-![]() ,0],求函数f(x)的值域.
,0],求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(ax2+2x+3).
(1)若f(x)定义域为R,求a的取值范围;
(2)若f(1)=1,求f(x)的单调区间;
(3)是否存在实数a,使f(x)的最小值为0?若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个结论:
①命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;
”;
②命题“若![]() ,则
,则![]() 且
且![]() ”的否定是“若
”的否定是“若![]() ,则
,则![]() ”;
”;
③命题“若![]() ,则
,则![]() 或
或![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() 或
或![]() ”;
”;
④若“![]() 是假命题,
是假命题,![]() 是真命题”,则命题
是真命题”,则命题![]() ,
,![]() 一真一假.
一真一假.
其中正确结论的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com