
【题目】已知四棱锥![]() 的底面ABCD是菱形,且
的底面ABCD是菱形,且![]() ,
,![]() 是等边三角形.
是等边三角形.
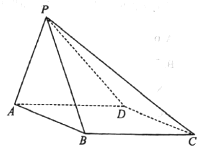
(Ⅰ)证明:![]() ;
;
(Ⅱ)若平面![]() 平面ABCD,求二面
平面ABCD,求二面![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
(I)取AB的中点O,连接OP,OD,BD,利用等比三角形的性质得到![]() ,利用有一个角是
,利用有一个角是![]() 的菱形的几何性质,证得
的菱形的几何性质,证得![]() ,由此证得
,由此证得![]() 平面
平面![]() ,从而证得
,从而证得![]() .
.
(II)证得![]() ,结合
,结合![]() ,以
,以![]() 为原点,建立空间直角坐标系,通过计算平面
为原点,建立空间直角坐标系,通过计算平面![]() 和平面
和平面![]() 的法向量,求得二面角的余弦值.
的法向量,求得二面角的余弦值.
(Ⅰ)证明:取AB的中点O,连接OP,OD,BD
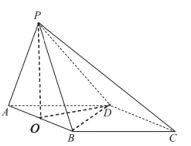
∵![]() 是等边三角形,∴
是等边三角形,∴![]()
又∵四边形ABCD是菱形,![]()
∴![]() 是等边三角形
是等边三角形
∴![]()
∵![]() ,PO,
,PO,![]() 平面POD
平面POD
∴![]() 平面POD
平面POD
∵![]() 平面POD
平面POD
∴![]()
(Ⅱ)∵平面![]() 平面ABCD,平面
平面ABCD,平面![]() 平面
平面![]() ,
,![]() ∴
∴![]() 平面ABCD,∴
平面ABCD,∴![]()
以O为原点,建立如图所示的空间直角坐标系O-xyz,
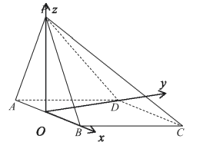
设![]()
平面PAB的一个法向量为![]() ,
,![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
设平面PBC的一个法向量为![]() ,则
,则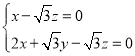
令![]() ,得
,得![]() ,
,![]()
∴![]()
设二面角![]() 的平面角为
的平面角为![]() ,
,![]() 为钝角
为钝角
∴![]()


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,圆
,圆![]() .
.
(Ⅰ)![]() 是抛物线
是抛物线![]() 的焦点,
的焦点,![]() 是抛物线
是抛物线![]() 上的定点,
上的定点,![]() ,求抛物线
,求抛物线![]() 的方程;
的方程;
(Ⅱ)在(Ⅰ)的条件下,过点![]() 的直线
的直线![]() 与圆
与圆![]() 相切,设直线
相切,设直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,则在
两点,则在![]() 轴上是否存在点
轴上是否存在点![]() 使
使![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,智能手机的更新换代极其频繁和快速,而青少年对新事物的追求更是强烈,为了调查大学生更换手机的时间,现对某大学中的大学生使用一部手机的年限进行了问卷调查,并从参与调查的大学生中抽取了男生、女生各![]() 人进行抽样分析,制成如下的频率分布直方图.
人进行抽样分析,制成如下的频率分布直方图.

(1)根据频率分布直方图,估计男大学生使用手机年限的中位数和女大学生使用手机年限的众数;
(2)根据频率分布直方图,求出男大学生和女大学生使用手机年限的平均值,并分析比较男大学生和女大学生哪个群体更换手机的频率更高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
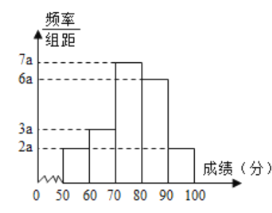
(1)求频率分布直方图中![]() 的值;
的值;
(2)估计总体中成绩落在![]() 中的学生人数;
中的学生人数;
(3)根据频率分布直方图估计![]() 名学生数学考试成绩的众数,中位数.
名学生数学考试成绩的众数,中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某共享单车经营企业欲向甲市投放单车,为制定适宜的经营策略,该企业首先在已投放单车的乙市进行单车使用情况调查.调查过程分随机问卷、整理分析及开座谈会三个阶段.在随机问卷阶段,A,B两个调查小组分赴全市不同区域发放问卷并及时收回;在整理分析阶段,两个调查小组从所获取的有效问卷中,针对15至45岁的人群,按比例随机抽取了300份,进行了数据统计,具体情况如下表:
组别 年龄 | A组统计结果 | B组统计结果 | ||
经常使用单车 | 偶尔使用单车 | 经常使用单车 | 偶尔使用单车 | |
| 27人 | 13人 | 40人 | 20人 |
| 23人 | 17人 | 35人 | 25人 |
| 20人 | 20人 | 35人 | 25人 |
(1)先用分层抽样的方法从上述300人中按“年龄是否达到35岁”抽出一个容量为60人的样本,再用分层抽样的方法将“年龄达到35岁”的被抽个体数分配到“经常使用单车”和“偶尔使用单车”中去.求这60人中“年龄达到35岁且偶尔使用单车”的人数;
(2)从统计数据可直观得出“是否经常使用共享单车与年龄(记作![]() 岁)有关”的结论.在用独立性检验的方法说明该结论成立时,为使犯错误的概率尽可能小,年龄
岁)有关”的结论.在用独立性检验的方法说明该结论成立时,为使犯错误的概率尽可能小,年龄![]() 应取25还是35?请通过比较
应取25还是35?请通过比较![]() 的观测值的大小加以说明.
的观测值的大小加以说明.
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为正项等比数列,a1+a2=6,a3=8.
(1)求数列{an}的通项公式an;
(2)若bn=![]() ,且{bn}前n项和为Tn,求Tn.
,且{bn}前n项和为Tn,求Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我边防局接到情报,在海礁![]() 所在直线
所在直线![]() 的一侧点
的一侧点![]() 处有走私团伙在进行交易活动,边防局迅速派出快艇前去搜捕:如图,已知快艇出发位置在
处有走私团伙在进行交易活动,边防局迅速派出快艇前去搜捕:如图,已知快艇出发位置在![]() 的另一侧码头
的另一侧码头![]() 处,
处,![]() 公里,
公里,![]() 公里,
公里,![]() ;
;

(1)是否存在点![]() ,使快艇沿航线
,使快艇沿航线![]() 或
或![]() 的路程相等;如存在,则建立适当的直角坐标系,求出点
的路程相等;如存在,则建立适当的直角坐标系,求出点![]() 的轨迹方程,且画出轨迹的大致图形;如不存在,请说明理由;
的轨迹方程,且画出轨迹的大致图形;如不存在,请说明理由;
(2)问走私船在怎样的区域上时,路线![]() 比路线
比路线![]() 的路程短,请说明理由.
的路程短,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆市第八中学校为了解学生喜爱运动是否与性别有关,从全校学生中随机抽取50名学生进行问卷调查,得到如图所示的![]() 列联表.
列联表.
喜爱运动 | 不喜爱运动 | 合计 | |
男生 | 22 | 8 | 30 |
女生 | 8 | 12 | 20 |
合计 | 30 | 20 | 50 |
附: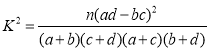 ,
,![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)能否有97.5%以上的把握认为“喜爱运动”与“性别”有关;
(2)用分层抽样的方法从被调查的20名女生中抽取5名进行问卷调查,求抽取喜爱运动的女生、不喜爱运动的女生各有多少的人;
(3)在(2)抽取的女生中,随机选出2人进行座谈,求至少有1名是喜爱运动的女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】线段AB外有一点C,∠ABC=60°,AB=200 km,汽车以80 km/h的速度由A向B行驶,同时摩托车以50 km/h的速度由B向C行驶,则运动开始________h后,两车的距离最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com