
【题目】抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,若
,若![]() 为抛物线上第一象限的一动点,过
为抛物线上第一象限的一动点,过![]() 作
作![]() 的垂线交准线
的垂线交准线![]() 于点
于点![]() ,交抛物线于
,交抛物线于![]() 两点.
两点.

(Ⅰ)求证:直线![]() 与抛物线相切;
与抛物线相切;
(Ⅱ)若点![]() 满足
满足![]() ,求此时点
,求此时点![]() 的坐标.
的坐标.
【答案】(I)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)设![]() ,由此可得直线
,由此可得直线![]() 的斜率,进而得到直线
的斜率,进而得到直线![]() 的斜率,由此得到
的斜率,由此得到![]() 的方程为
的方程为![]() ,令
,令![]() 可得点
可得点![]() 的坐标,于是可得直线
的坐标,于是可得直线![]() 的斜率.然后再由导数的几何意义得到在点A处的切线的斜率,比较后可得结论.(Ⅱ)由(Ⅰ)知
的斜率.然后再由导数的几何意义得到在点A处的切线的斜率,比较后可得结论.(Ⅱ)由(Ⅰ)知![]() ,直线
,直线![]() 的方程为
的方程为![]() ,将直线方程与椭圆方程联立消元后得到二次方程,结合根与系数的关系及
,将直线方程与椭圆方程联立消元后得到二次方程,结合根与系数的关系及![]() 可求得点A的坐标.
可求得点A的坐标.
(Ⅰ)由题意得焦点![]() .设
.设![]() ,
,
∴直线![]() 的斜率为
的斜率为![]() ,
,
由已知直线![]() 斜率存在,且直线
斜率存在,且直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∴直线![]() 的斜率为
的斜率为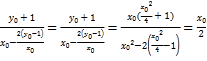 .
.
由![]() 得
得![]() ,
,
∴![]() ,即抛物线在点A处的切线的斜率为
,即抛物线在点A处的切线的斜率为![]() ,
,
∴直线![]() 与抛物线相切.
与抛物线相切.
(Ⅱ)由(Ⅰ)知![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
由 消去
消去![]() 整理得
整理得![]() ,
,
设![]() ,
,
则![]() .
.
由题意得直线![]() 的斜率为
的斜率为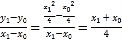 ,
,
直线![]() 的斜率为
的斜率为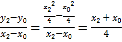 ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
整理得![]() ,
,
解得![]() 或
或![]() .
.
∵![]() ,
,
∴![]() ,
,
又![]() ,且
,且![]() ,
,
∴存在![]() ,使得
,使得![]() .
.


科目:高中数学 来源: 题型:
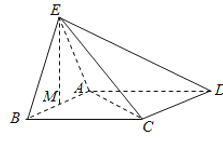
【题目】如图,正三角形ABE与菱形ABCD所在的平面互相垂直,![]() ,
,![]() ,M是AB的中点.
,M是AB的中点.
(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在线段EC上是否存在点P,使得直线AP与平面ABE所成的角为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
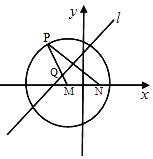
【题目】如图,圆![]() ,
,![]() 是圆M内一个定点,P是圆上任意一点,线段PN的垂直平分线l和半径MP相交于点Q,当点P在圆M上运动时,点Q的轨迹为曲线E
是圆M内一个定点,P是圆上任意一点,线段PN的垂直平分线l和半径MP相交于点Q,当点P在圆M上运动时,点Q的轨迹为曲线E
(1)求曲线E的方程;
(2)过点D(0,3)作直线m与曲线E交于A,B两点,点C满足![]() (O为原点),求四边形OACB面积的最大值,并求此时直线m的方程;
(O为原点),求四边形OACB面积的最大值,并求此时直线m的方程;
(3)已知抛物线![]() 上,是否存在直线与曲线E交于G,H,使得G,H的中点F落在直线y=2x上,并且与抛物线相切,若直线存在,求出直线的方程,若不存在,说明理由.
上,是否存在直线与曲线E交于G,H,使得G,H的中点F落在直线y=2x上,并且与抛物线相切,若直线存在,求出直线的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一项针对都市熟男(三线以上城市,![]() 岁男性)消费水平的调查显示,对于最近一年内是否购买过以下七类高价商品,全体被调查者,以及其中包括的1980年及以后出生(80后)被调查者,1980年以前出生(80前)被调查者回答“是”的比例分别如下:
岁男性)消费水平的调查显示,对于最近一年内是否购买过以下七类高价商品,全体被调查者,以及其中包括的1980年及以后出生(80后)被调查者,1980年以前出生(80前)被调查者回答“是”的比例分别如下:
全体被调查者 | 80后被调查者 | 80前被调查者 | |
电子产品 | 56.9% | 66.0% | 48.5% |
服装 | 23.0% | 24.9% | 21.2% |
手表 | 14.3% | 19.4% | 9.7% |
运动、户外用品 | 10.4% | 11.1% | 9.7% |
珠宝首饰 | 8.6% | 10.8% | 6.5% |
箱包 | 8.1% | 11.3% | 5.1% |
个护与化妆品 | 6.6% | 6.0% | 7.2% |
以上皆无 | 25.3% | 17.9% | 32.1% |
根据表格中数据判断,以下分析错误的是( )
A. 都市熟男购买比例最高的高价商品是电子产品
B. 从整体上看,80后购买高价商品的意愿高于80前
C. 80前超过3成一年内从未购买过表格中七类高价商品
D. 被调查的都市熟男中80后人数与80前人数的比例大约为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ,如果存在,求
,如果存在,求![]() 与平面
与平面![]() 所成角的正弦值;如果不存在,请说明理由.
所成角的正弦值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为椭圆
为椭圆![]() 上任意一点,且
上任意一点,且![]() 的最小值为0.
的最小值为0.
(1)求椭圆![]() 的方程;
的方程;
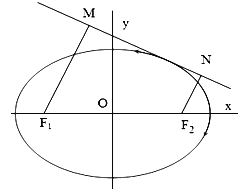
(2)如图,动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,点
有且仅有一个公共点,点![]() ,
,![]() 是直线
是直线![]() 上的两点,且
上的两点,且![]() ,
,![]() ,求四边形
,求四边形![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() ,四点
,四点![]() ,
,![]() ,
,![]() ,
,![]() 中恰有三点在椭圆
中恰有三点在椭圆![]() 上.
上.
(I)求椭圆![]() 的标准方程;
的标准方程;
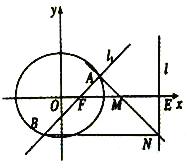
(Ⅱ)过![]() 的右焦点
的右焦点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 为线段
为线段![]() 的中点,过点
的中点,过点![]() 作直线
作直线![]() 于点
于点![]() .证明:
.证明:![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com