

| 应该取消 | 应该保留 | 无所谓 | ||
| 在校学生 | 2100人 | 120人 | y人 | ||
| 社会人士 | 600人 | x人 | z人 |
| ξ | 1 | 2 | 3 |
| P | 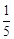 | 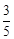 | 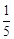 |
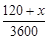 =0.05,解得x=60.这样可得持“无所谓”态度的人数,共有3600-2100-120-600-60=720人.分层抽样实质上就是按比例抽样,所以应在“无所谓”态度抽取720×
=0.05,解得x=60.这样可得持“无所谓”态度的人数,共有3600-2100-120-600-60=720人.分层抽样实质上就是按比例抽样,所以应在“无所谓”态度抽取720× =72人.(2)由(1)知持“应该保留”态度的人一共有180人,按比例计算可得在所抽取的6人中,在校学生为
=72人.(2)由(1)知持“应该保留”态度的人一共有180人,按比例计算可得在所抽取的6人中,在校学生为 =4人,社会人士为
=4人,社会人士为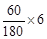 =2人.将这6人平均分成两组,则第一组在校学生人数ξ=1,2,3.这是一个超几何分布,根据超几何分布的概率公式即可得其分布列,进而求得其期望.
=2人.将这6人平均分成两组,则第一组在校学生人数ξ=1,2,3.这是一个超几何分布,根据超几何分布的概率公式即可得其分布列,进而求得其期望. 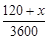 =0.05,解得x=60. 2分
=0.05,解得x=60. 2分 =72人. 6分
=72人. 6分 =4人,社会人士为
=4人,社会人士为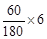 =2人,
=2人,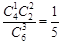 ,P(ξ=2)=
,P(ξ=2)=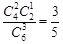 ,P(ξ=3)=
,P(ξ=3)= ,
,| ξ | 1 | 2 | 3 |
| P | 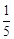 | 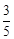 | 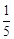 |
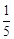 +2×
+2×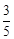 +3×
+3×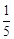 =2. 12分
=2. 12分

 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
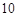 分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;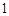 ;
;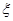 服从正态分布
服从正态分布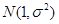
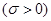 ,若
,若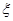 位于区域
位于区域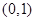 内的概率为
内的概率为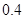 ,则
,则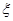 位于区域
位于区域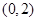 内的概率为
内的概率为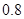 ;
;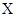 与
与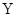 的随机变量K2的观测值k来说,k越小,判断“
的随机变量K2的观测值k来说,k越小,判断“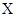 与
与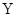 有关系”的把握越大.其中真命题的序号为( )
有关系”的把握越大.其中真命题的序号为( )| A.①④ | B.②④ | C.①③ | D.②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的列联表如下:
的列联表如下:| | 不及格 | 及格 | 总计 |
| 甲班 | a | b | |
| 乙班 | c | d | |
| 总计 | | | |
 ;
;
| P(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
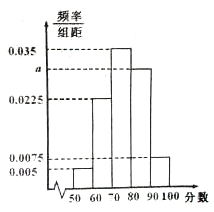
| API | 0~50 | 51~ 100 | 101~ 150 | 151~ 200 | 201~ 250 | 251~ 300 | >300 |
| 级 别 | Ⅰ | Ⅱ | Ⅲ1 | Ⅲ2 | Ⅳ1 | Ⅳ2 | Ⅴ |
| 状 况 | 优 | 良 | 轻微 污染 | 轻度 污染 | 中度 污染 | 中度 重污染 | 重度 污染 |
| |  |  |  |  |  | ||

 +
+ +
+ +
+ +
+ =
= ,365=73×5).
,365=73×5).查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
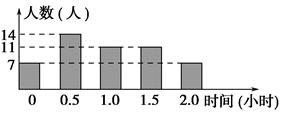
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2]),其中
)2]),其中 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| | 积极参加班级工作 | 不太主动参加班级工作 | 合计 |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com