
【题目】已知函数![]() 是奇函数(
是奇函数(![]() ).
).
(1)求实数![]() 的值;
的值;
(2)试判断函数![]() 在
在![]() 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:高中数学 来源: 题型:
【题目】2019年,河北等8省公布了高考改革综合方案将采取“![]() ”模式,即语文、数学、英语必考,然后考生先在物理、历史中选择1门,再在思想政治、地理、化学、生物中选择2门.为了更好进行生涯规划,张明同学对高一一年来的七次考试成绩进行统计分析,其中物理、历史成绩的茎叶图如图所示.
”模式,即语文、数学、英语必考,然后考生先在物理、历史中选择1门,再在思想政治、地理、化学、生物中选择2门.为了更好进行生涯规划,张明同学对高一一年来的七次考试成绩进行统计分析,其中物理、历史成绩的茎叶图如图所示.
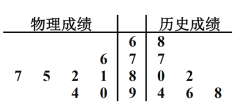
(1)若张明同学随机选择3门功课,求他选到物理政治两门功课的概率;
(2)试根据茎叶图分析张明同学应在物理和历史中选择哪个学科?并阐述理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M(x,y)满足![]()
(1)求点M的轨迹E的方程;
(2)设过点N(﹣1,0)的直线l与曲线E交于A,B两点,若△OAB的面积为![]() (O为坐标原点).求直线l的方程.
(O为坐标原点).求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,前n项和为Sn(n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.
(1)求{an}和{bn}的通项公式;
(2)求数列{a2nbn}的前n项和(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是实数,函数
是实数,函数![]() .
.
(Ⅰ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅱ)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,当
,当![]() 时,若
时,若![]() 在
在![]() 内恒成立,则称点
内恒成立,则称点![]() 为函数
为函数![]() 的“平衡点”.当
的“平衡点”.当![]() 时,试问函数
时,试问函数![]() 是否存在“平衡点”?若存在,请求出“平衡点”的横坐标;若不存在,请说明理由.
是否存在“平衡点”?若存在,请求出“平衡点”的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四名同学组成一个4![]() 100米接力队,老师要安排他们四人的出场顺序,以下是他们四人的要求:甲:我不跑第一棒和第二棒;乙:我不跑第一棒和第四棒;丙:我也不跑第一棒和第四棒;丁:如果乙不跑第二棒,我就不跑第一棒.老师听了他们四人的对话,安排了一种合理的出场顺序,满足了他们的所有要求,据此我们可以断定在老师安排的出场顺序中跑第三棒的人是_________.
100米接力队,老师要安排他们四人的出场顺序,以下是他们四人的要求:甲:我不跑第一棒和第二棒;乙:我不跑第一棒和第四棒;丙:我也不跑第一棒和第四棒;丁:如果乙不跑第二棒,我就不跑第一棒.老师听了他们四人的对话,安排了一种合理的出场顺序,满足了他们的所有要求,据此我们可以断定在老师安排的出场顺序中跑第三棒的人是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<![]() )的图象如图所示,为了得到g(x)=Acosωx的图象,只需把y=f(x)的图象上所有的点( )
)的图象如图所示,为了得到g(x)=Acosωx的图象,只需把y=f(x)的图象上所有的点( )

A. 向右平移![]() 个单位长度 B. 向左平移
个单位长度 B. 向左平移![]() 个单位长度
个单位长度
C. 向右平移![]() 个单位长度 D. 向左平移
个单位长度 D. 向左平移![]() 个单位长度
个单位长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com