
【题目】已知函数f(x)及其导数f′(x),若存在x0,使得f(x0)=f′(x0),则称x0是f(x)的一个“巧值点”,则下列函数中有“巧值点”的是________.
①f(x)=x2;②f(x)=e-x;③f(x)=lnx;④f(x)=tanx;⑤![]() .
.
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an=2+2cos2![]() ,n∈N*,等差数列{bn}满足a1=2b1,a2=b2.
,n∈N*,等差数列{bn}满足a1=2b1,a2=b2.
(1)求bn;
(2)记cn=a2n-1b2n-1+a2nb2n,求cn;
(3)求数列{anbn}前2n项和S2n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义在
是定义在![]() 上的单调函数,且对于任意正数
上的单调函数,且对于任意正数![]() 有
有![]() ,已知
,已知![]() ,若一个各项均为正数的数列
,若一个各项均为正数的数列![]() 满足
满足![]() ,其中
,其中![]() 是数列
是数列![]() 的前
的前![]() 项和,则数列
项和,则数列![]() 中第18项
中第18项![]() ( )
( )
A. ![]() B. 9 C. 18 D. 36
B. 9 C. 18 D. 36
查看答案和解析>>
科目:高中数学 来源: 题型:
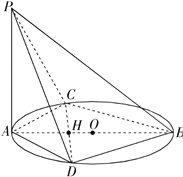
【题目】已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面.
(Ⅰ)求证:PB⊥CD;
(Ⅱ)若PB=![]() ,∠PBA=
,∠PBA=![]() ,∠CAD=
,∠CAD=![]() ,求H到平面PBD的距离.
,求H到平面PBD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的首项a1=1,公差d>0.且a2,a5,a14分别是等比数列{bn}的b2,b3,b4.
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}对任意自然数n均有![]() 成立,求c1+c2+…+c2016的值.
成立,求c1+c2+…+c2016的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,f(x+1)为奇函数,f(0)=0,当x∈(0,1]时,f(x)=log2x,则在区间(8,9)内满足方程f(x)+2=![]() 的实数x为( )
的实数x为( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=![]() AD,E,F分别为线段AD,PC的中点.
AD,E,F分别为线段AD,PC的中点.
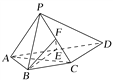
(1)求证:AP∥平面BEF;
(2)求证:BE⊥平面PAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为线段
分别为线段![]() 上的点,且
上的点,且![]() ,
, ![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的锐二面角.
所成的锐二面角.
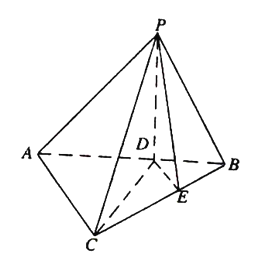
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com