
【题目】如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,点O为对角线BD的中点,点E,F分别为棱PC,PD的中点,已知PA⊥AB,PA⊥AD.
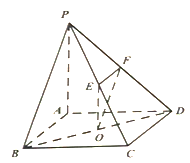
(1)求证:直线PB∥平面OEF;
(2)求证:平面OEF⊥平面ABCD.
【答案】详见解析
【解析】
(1)根据O为PB中点,F为PD中点,所以,PB∥FO,之后应用线面垂直的判定定理证得结果;
(2)根据题意,得到PA∥OE,结合题中所给的条件因为PA⊥AB,PA⊥AD,AB∩AD=A,可得PA⊥平面ABCD,从而得到OE⊥平面ABCD,根据面面垂直的判定定理证得结果.
(1)O为PB中点,F为PD中点,所以,PB∥FO
而PB![]() 平面OEF,FO
平面OEF,FO![]() 平面OEF,
平面OEF,
∴ PB∥平面OEF.
(2)连结AC,因为ABCD为平行四边形,
∴AC与BD交于点O,O为AC中点,又E为PC中点,
∴ PA∥OE,
因为PA⊥AB,PA⊥AD,AB∩AD=A,
∴ PA⊥平面ABCD,
∴ OE⊥平面ABCD
又OE![]() 平面OEF,
平面OEF,
∴ 平面OEF⊥平面ABCD


科目:高中数学 来源: 题型:
【题目】网购是现在比较流行的一种购物方式,现随机调查50名个人收入不同的消费者是否喜欢网购,调查结果表明:在喜欢网购的25人中有18人是低收入的人,另外7人是高收入的人,在不喜欢网购的25人中有6人是低收入的人,另外19人是高收入的人.
喜欢网购 | 不喜欢网购 | 总计 | |
低收入的人 | |||
高收入的人 | |||
总计 |
(Ⅰ)试根据以上数据完成![]() 列联表,并用独立性检验的思想,指出有多大把握认为是否喜欢网购与个人收入高低有关系;
列联表,并用独立性检验的思想,指出有多大把握认为是否喜欢网购与个人收入高低有关系;
(Ⅱ)将5名喜欢网购的消费者编号为1、2、3、4、5,将5名不喜欢网购的消费者编号也记作1、2、3、4、5,从这两组人中各任选一人进行交流,求被选出的2人的编号之和为2的倍数的概率.
参考公式:
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地要建造一个边长为2(单位:![]() )的正方形市民休闲公园
)的正方形市民休闲公园![]() ,将其中的区域
,将其中的区域![]() 开挖成一个池塘,如图建立平面直角坐标系后,点
开挖成一个池塘,如图建立平面直角坐标系后,点![]() 的坐标为
的坐标为![]() ,曲线
,曲线![]() 是函数
是函数![]() 图像的一部分,过边
图像的一部分,过边![]() 上一点
上一点![]() 在区域
在区域![]() 内作一次函数
内作一次函数![]() (
(![]() )的图像,与线段
)的图像,与线段![]() 交于点
交于点![]() (点
(点![]() 不与点
不与点![]() 重合),且线段
重合),且线段![]() 与曲线
与曲线![]() 有且只有一个公共点
有且只有一个公共点![]() ,四边形
,四边形![]() 为绿化风景区.
为绿化风景区.
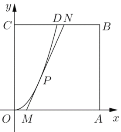
(1)求证:![]() ;
;
(2)设点![]() 的横坐标为
的横坐标为![]() ,
,
①用![]() 表示
表示![]() 、
、![]() 两点的坐标;
两点的坐标;
②将四边形![]() 的面积
的面积![]() 表示成关于
表示成关于![]() 的函数
的函数![]() ,并求
,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 F (x) = e x 满足 F ( x) = g ( x) + h( x) ,且 g ( x), h( x) 分别是定义在 R 上的偶函数和奇函数.
(1)求函数 h(x)的反函数;
(2)已知(x) = g(x 1),若函数(x)在 [1,3]上满足(2 a+1) ![]() ,求实数 a 的取值范围;
,求实数 a 的取值范围;
(3)若对于任意 x ∈(0,2]不等式 g(2x) ah(x) ≥ 0 恒成立,求实数 a 的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙、丙三位同学在某次考试中总成绩列前三名,有![]() ,
,![]() ,
,![]() 三位学生对其排名猜测如下:
三位学生对其排名猜测如下:![]() :甲第一名,乙第二名;
:甲第一名,乙第二名;![]() :丙第一名;甲第二名;
:丙第一名;甲第二名;![]() :乙第一名,甲第三名.成绩公布后得知,
:乙第一名,甲第三名.成绩公布后得知,![]() ,
,![]() ,
,![]() 三人都恰好猜对了一半,则第一名是__________.
三人都恰好猜对了一半,则第一名是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱柱![]() 的侧面
的侧面![]() 是圆柱的轴截面,C是圆柱底面圆周上不与A、B重合的一个点。
是圆柱的轴截面,C是圆柱底面圆周上不与A、B重合的一个点。
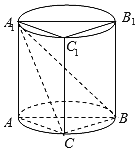
(1)若圆柱的轴截面是正方形,当点C是弧AB的中点时,求异面直线![]() 与AB的所成角的大小(结果用反三角函数值表示);
与AB的所成角的大小(结果用反三角函数值表示);
(2)当点C是弧AB的中点时,求四棱锥![]() 体积与圆柱体积的比.
体积与圆柱体积的比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月郑州市被国务院确定为全国46个生活垃圾分类处理试点城市之一,此后由郑州市城市管理局起草公开征求意见,经专家论证,多次组织修改完善,数易其稿,最终形成《郑州市城市生活垃圾分类管理办法》(以下简称《办法》).《办法》已于2019年9月26日被郑州市人民政府第35次常务会议审议通过,并于2019年12月1日开始施行.《办法》中将郑州市生活垃圾分为厨余垃圾、可回收垃圾、有害垃圾和其他垃圾4类.为了获悉高中学生对垃圾分类的了解情况,某中学设计了一份调查问卷,500名学生参加测试,从中随机抽取了100名学生问卷,记录他们的分数,将数据分成7组:![]() ,
,![]() ,…,
,…,![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:
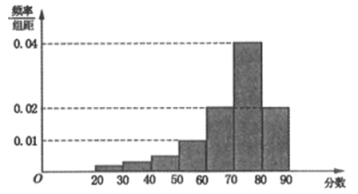
(1)从总体的500名学生中随机抽取一人,估计其分数不低于60的概率;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间![]() 内的学生人数,
内的学生人数,
(3)学校环保志愿者协会决定组织同学们利用课余时间分批参加“垃圾分类,我在实践”活动,以增强学生的环保意识.首次活动从样本中问卷成绩低于40分的学生中随机抽取2人参加,已知样本中分数小于40的5名学生中,男生3人,女生2人,求抽取的2人中男女同学各1人的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com