
分析 根据对数的运算性质计算即可.
解答 解:(1)(lg5)2+lg2•lg5+lg2=lg5(lg5+lg2)+lg2=lg5+lg2=1;
(2)lg5(lg8+lg1000)+(lg2${\;}^{\sqrt{3}}$)2+lg0.06+lg$\frac{1}{6}$,
=lg5(3lg2+3)+3lg22+lg(0.06×$\frac{1}{6}$),
=3lg5lg2+3lg5+3lg22+lg0.01,
=3lg2(lg5+lg2)+3lg5-2,
=3lg2+3lg5-2,
=3(lg2+lg5)-2,
=3-2,
=1.
点评 本题考查了对数的运算性质,灵活利用lg2+lg5=1是关键属于基础题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 4 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
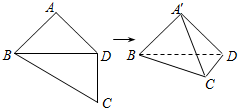 如图,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′BCD,使得平面A′BD⊥平面BDC,给出下列四个结论,其中正确的有( )
如图,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′BCD,使得平面A′BD⊥平面BDC,给出下列四个结论,其中正确的有( )| A. | A′B⊥CD | |
| B. | 四面体A′BCD的体积为$\frac{1}{2}$ | |
| C. | A′C与BD所成的角为60° | |
| D. | 四面体A′BCD的外接球的表面积为$\frac{7π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
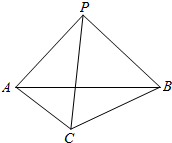 如图,在三棱锥P-ABC中,PA=PB=$\sqrt{6}$,PA⊥PB,AB⊥BC,∠BAC=30°,平面PAB⊥平面ABC.
如图,在三棱锥P-ABC中,PA=PB=$\sqrt{6}$,PA⊥PB,AB⊥BC,∠BAC=30°,平面PAB⊥平面ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com