
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).M是曲线
为参数).M是曲线![]() 上的动点,将线段OM绕O点顺时针旋转
上的动点,将线段OM绕O点顺时针旋转![]() 得到线段ON,设点N的轨迹为曲线
得到线段ON,设点N的轨迹为曲线![]() .以坐标原点O为极点,
.以坐标原点O为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,若射线![]() 与曲线
与曲线![]() 分别交于A, B两点(除极点外),且有定点
分别交于A, B两点(除极点外),且有定点![]() ,求
,求![]() 的面积.
的面积.
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1千多年.在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑指四个面均为直角三角形的四面体.如图,在堑堵![]() 中,
中,![]() .
.

(1)求证:四棱锥![]() 为阳马;并判断四面体
为阳马;并判断四面体![]() 是否为鳖臑,若是,请写出各个面的直角(要求写出结论).
是否为鳖臑,若是,请写出各个面的直角(要求写出结论).
(2)若![]() ,当阳马
,当阳马![]() 体积最大时,求二面角
体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个判断正确的是______(写出所有正确判断的序号.)
①函数![]() 是奇函数,但不是偶函数;
是奇函数,但不是偶函数;
②函数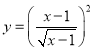 与函数
与函数![]() 表示同一个函数;
表示同一个函数;
③已知函数![]() 图象的一条对称轴为
图象的一条对称轴为![]() ,则
,则![]() 的值为
的值为![]() ;
;
④设函数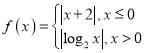 ,若关于
,若关于![]() 的方程
的方程![]() 有四个不同的解
有四个不同的解![]() ,且
,且![]() ,则
,则![]() 的值为
的值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第28届金鸡百花电影节将在福建省厦门市举办,近日首批影展片单揭晓,《南方车站的聚会》《春江水暖》《第一次的离别》《春潮》《抵达之谜》五部优秀作品将在电影节进行展映.若从这五部作品中随机选择两部放在展映的前两位,则《春潮》与《抵达之谜》至少有一部被选中的概率为 _____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个口袋有![]() 个白球,
个白球,![]() 个黑球,这些球除颜色外全部相同,现将口袋中的球随机逐个取出,并依次放入编号为
个黑球,这些球除颜色外全部相同,现将口袋中的球随机逐个取出,并依次放入编号为![]() ,
,![]() ,
,![]() ,
,![]() 的抽屉内.
的抽屉内.
(1)求编号为![]() 的抽屉内放黑球的概率;
的抽屉内放黑球的概率;
(2)口袋中的球放入抽屉后,随机取出两个抽屉中的球,求取出的两个球是一黑一白的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() :
:![]() ,圆
,圆![]() :
:![]() .
.
(1)求![]() 的取值范围,并求出圆心坐标;
的取值范围,并求出圆心坐标;
(2)若圆![]() 的半径为1,过点
的半径为1,过点![]() 作圆
作圆![]() 的切线,求切线的方程;
的切线,求切线的方程;
(3)有一动圆![]() 的半径为1,圆心在
的半径为1,圆心在![]() 上,若动圆
上,若动圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分为5组:![]()
![]()
![]() 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.
(I)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的概率;
(II)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
![]()
![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
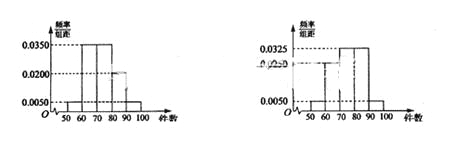
25周岁以上组 25周岁以下组
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com