
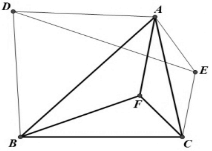
 已知,△ABC内有一点F,分别以AB、AC为底边向外作等腰三角形DAB、AEC,且∠BAD=∠BCF,∠ACE=∠CBF.求证:DE平分AF.
已知,△ABC内有一点F,分别以AB、AC为底边向外作等腰三角形DAB、AEC,且∠BAD=∠BCF,∠ACE=∠CBF.求证:DE平分AF. 分析 如图,延长AD至M,延长AE至N,使得AD=MD,AE=EN,连接MB,NC、MN,作AP⊥MN,连接PB,PC,PF,利用等腰三角形与四点共圆的性质先证明点F在直线MN上,再利用三角形中位线定理即可证明.
解答 证明:如图,延长AD至M,延长AE至N,使得AD=MD,AE=EN,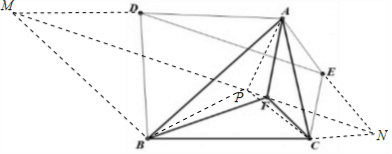
连接MB,NC、MN,作AP⊥MN,
连接PB,PC,PF,先证明点F在直线MN上,∵AD=MD=BD,∴MB⊥AB,
同理可得:CN⊥AC.又AP⊥MN,
可得A,M,B,P四点共圆,
可得A,N,C,P四点共圆,
可得:∠MPB=∠MAB=∠FCB,∠CPN=∠NAC=∠FBC,
∴∠BPC=180°-∠FBC-∠FCB,又∠BFPC=180°-∠PBC-∠FCB,
∴∠BPC=∠BFC,∴B,C,F,P四点共圆,
∴∠BPF+∠BCF=180°,∴∠BPM+∠BPF=180°,
∴M,P,F三点共线.即点F在直线MN上.
又AD=MD,AE=EN,
∴DE为△AMN的中位线,∴DE平分AF.
点评 本题考查了等腰三角形与四点共圆的性质、三角形中位线定理、三角形内角和定理,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com