
【题目】若Sn为等差数列{an}的前n项和,且a1=1,S10=55.记bn=[lnan],其中[x]表示不超过x的最大整数,如[0.9]=0,[lg99]=1.则数列{bn}的前2017项和为 .
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和为Sn , 且 ![]() (a∈N+).
(a∈N+).
(1)求a的值及数列{an}的通项公式;
(2)设 ![]() ,求{bn}的前n项和Tn .
,求{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点在直角坐标系的原点,极轴与x轴的正半轴重合,曲线C的极坐标方程为ρ2cos2θ+3ρ2sin2θ=3,直线l的参数方程为 ![]() .试在曲线C上求一点M,使它到直线l的距离最大.
.试在曲线C上求一点M,使它到直线l的距离最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,椭圆C: ![]() 的离心率是
的离心率是 ![]() ,
,
抛物线E:x2=4y的焦点F是C的一个顶点.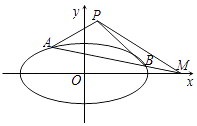
(1)求椭圆C的方程;
(2)设与坐标轴不重合的动直线l与C交于不同的两点A和B,与x轴交于点M,且 ![]() 满足kPA+kPB=2kPM , 试判断点M是否为定点?若是定点求出点M的坐标;若不是定点请说明理由.
满足kPA+kPB=2kPM , 试判断点M是否为定点?若是定点求出点M的坐标;若不是定点请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合L={l|l与直线y=x相交,且以交点的横坐标为斜率}.若直线l′∈L,点P(﹣1,2)到直线l′的最短距离为r,则以点P为圆心,r为半径的圆的标准方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学为研究函数 ![]() 的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC,点P是边BC上的一个动点,设CP=x,则AP+PF=f(x).请你参考这些信息,推知函数f(x)的值域是 .
的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC,点P是边BC上的一个动点,设CP=x,则AP+PF=f(x).请你参考这些信息,推知函数f(x)的值域是 . 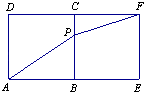
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aex﹣2x﹣2a,且a∈[1,2],设函数f(x)在区间[0,ln2]上的最小值为m,则m的取值范围是( )
A.[﹣2,﹣2ln2]
B.[﹣2,﹣ ![]() ]
]
C.[﹣2ln2,﹣1]
D.[﹣1,﹣ ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com