
分析 (1)求出f(x)的导数,求得切线的斜率,由两直线平行的条件:斜率相等,解方程可得切点的坐标;
(2)由题意可得x2-ax+1>0恒成立,运用判别式小于0,解不等式即可得到所求范围.
解答 解:(1)函数f(x)=x3+x-2的导数为f′(x)=3x2+1,
设P0(m,n),由题意可得3m2+1=4,解得m=-1(1舍去),
n=-1-1-2=-4,即有P0(-1,-4);
(2)对任意的x∈R,都有g(x)>f(x),
即为x2-ax+1>0恒成立,
即有△<0,即为a2-4<0,
解得-2<a<2.
则实数a的取值范围为(-2,2).
点评 本题考查导数的运用:求切线的斜率,考查两直线平行的条件,同时考查不等式恒成立问题的解法,考查运算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,三棱锥P-ABC中,∠ABC为直角,PB⊥平面ABC,AB=BC=PB=1,M为PC的中点,N为AC中点,以{$\overrightarrow{BA}$,$\overrightarrow{BC}$,$\overrightarrow{BP}$}为基底,则$\overrightarrow{MN}$的坐标为$(\frac{1}{2},0,-\frac{1}{2})$.
如图所示,三棱锥P-ABC中,∠ABC为直角,PB⊥平面ABC,AB=BC=PB=1,M为PC的中点,N为AC中点,以{$\overrightarrow{BA}$,$\overrightarrow{BC}$,$\overrightarrow{BP}$}为基底,则$\overrightarrow{MN}$的坐标为$(\frac{1}{2},0,-\frac{1}{2})$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,PA=BC=AC=4,D为PC的中点.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,PA=BC=AC=4,D为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
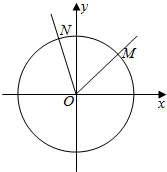 如图,在直角坐标系xOy中,锐角α的顶点是原点,始边与x轴非负半轴重合,终边交单位圆于点M(x1,y1),将角α的终边按逆时针方向旋转$\frac{π}{3}$,交单位圆于点M(x2,y2).记f(α)=y1+y2.
如图,在直角坐标系xOy中,锐角α的顶点是原点,始边与x轴非负半轴重合,终边交单位圆于点M(x1,y1),将角α的终边按逆时针方向旋转$\frac{π}{3}$,交单位圆于点M(x2,y2).记f(α)=y1+y2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{27}{25}$ | B. | -$\frac{25}{3}$ | C. | -$\frac{27}{25}$或-$\frac{25}{3}$ | D. | $\frac{25}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
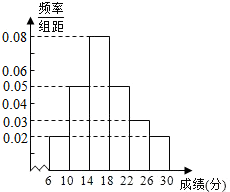 某省去年高三200000考生英语听力考试成绩服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图.
某省去年高三200000考生英语听力考试成绩服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com