
【题目】若函数f(x)=x2﹣2ax+3为定义在[﹣2,2]上的函数.
(1)当a=1时,求f(x)的最大值与最小值;
(2)若f(x)的最大值为M,最小值为m,函数g(a)=M﹣m,求g(a)的解析式,并求其最小值.
【答案】
(1)解:当a=1时,f(x)=x2﹣2x+3的对称轴为x=1,
∴f(x)在[﹣2,1]上单调递减,在(1,2]上单调递增,
∴f(x)max=f(﹣2)=4+4+3=11,f(x)min=f(1)=1﹣2+3=2
(2)解:∵f(x)=x2﹣2ax+3的对称轴为x=a,
当a≤﹣2时,f(x)在[﹣2,2]上单调递增,
∴f(x)min=f(﹣2)=4+4a+3=4a+7,f(x)max=f(2)=﹣4a+7,
∴g(a)=M﹣m=﹣4a+7﹣4a﹣7=﹣8a,
当a≥2时,f(x)在[﹣2,2]上单调递减,
∴f(x)max=f(﹣2)=4a+7,f(x)min=f(2)=﹣4a+7,
∴g(a)=M﹣m=4a+7﹣4a﹣7=8a,
当﹣2≤a<0时,f(x)在[﹣2,a)上单调递减,在(a,2]上单调递增,
∴f(x)max=f(2)=﹣4a+7,f(x)min=f(a)=﹣a2+3,
∴g(a)=M﹣m=﹣4a+a2+3,
当0≤a<2时,f(x)在[﹣2,a)上单调递减,在(a,2]上单调递增,
∴f(x)max=f(﹣2)=4a+7,f(x)min=f(a)=﹣a2+3,
∴g(a)=M﹣m=4a+a2+3,
∴g(a)= 
当a≥2,g(a)min=16,
当0≤a<2时,g(a)min=g(0)=3,
当﹣2<a<0时,g(a)min=g(0)=3,
当a≤﹣2时,g(a)min=16,
综上所述g(a)min=3
【解析】(1)根据二次函数的性质即可求出函数的最值,(2)需要分类讨论,根据对称轴和函数的单调性即可求出最值,即可求出g(a)的解析式,再分别求出最小值,即可得到答案.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.


科目:高中数学 来源: 题型:
【题目】如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点. 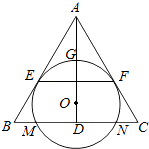
(1)证明:EF∥BC;
(2)若AG等于⊙O的半径,且AE=MN=2 ![]() ,求四边形EBCF的面积.
,求四边形EBCF的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2|x|﹣3a
(1)当a=1时,在所给坐标系中,画出函数f(x)的图象,并求f(x)的单调递增区间
(2)若直线y=1与函数f(x)的图象有4个交点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2x2+ax+2=0,a∈R},B={x|x2+3x+2a=0,a∈R},A∩B={2}且A∪B=I,则(IA)∪(IB)=( )
A.{﹣5, ![]() }
}
B.{﹣5, ![]() ,2}
,2}
C.{﹣5,2}
D.{ ![]() ,2}
,2}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,若对于在定义域内存在实数
,若对于在定义域内存在实数![]() 满足
满足![]() ,则称函数
,则称函数![]() 为“局部奇函数”.若函数
为“局部奇函数”.若函数![]() 是定义在
是定义在![]() 上的“局部奇函数”,则实数
上的“局部奇函数”,则实数![]() 的取值范围是( )
的取值范围是( )
A. [1﹣![]() ,1+
,1+![]() ) B. [﹣1,2] C. [﹣2
) B. [﹣1,2] C. [﹣2![]() ,2
,2![]() ] D. [﹣2
] D. [﹣2![]() ,1﹣
,1﹣![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com