
����Ŀ��������ʾ:����ABC��һ��뾶Ϊ2ǧ�ף�Բ�Ľ�Ϊ60���ķ羰����P���ڻ�BC�ϣ������ڷ羰���й滮����������ҵ�ֵ�PQ��QR��RP��Ҫ��ֵ�PQ��AB��ֱ���ֵ�PR��AC��ֱ��ֱ��PQ��ʾ�������ֵ���
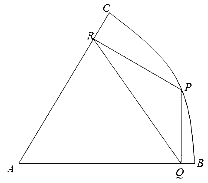
(1)���Pλ�ڻ�BC���е㣬�������ֵ����ܳ��ȣ�
(2)���ڻ�����ԭ�������ֵ�PQ��PR��QRÿ���ܲ����ľ���Ч��ֱ�Ϊÿǧ��300��Ԫ��200��Ԫ��400��Ԫ����:�������ֵ�ÿ���ܲ����ľ�����Ч�����Ϊ���٣�(��ȷ��1��Ԫ)
���𰸡���1��![]() ����2��1222��Ԫ
����2��1222��Ԫ
��������
��1����![]() ��
Ϊ��![]() �Ľ�ƽ�����ϣ����ü��ι�ϵ���ֱ��ʾ
�Ľ�ƽ�����ϣ����ü��ι�ϵ���ֱ��ʾ![]() ��
��![]() ��
��![]() ������
������
��������ֵ����ܳ��ȣ���2����![]() ��
��![]() ���������Ǻ�����ϵ�����Ҷ������������
���������Ǻ�����ϵ�����Ҷ������������![]() ��
��![]() ��
��![]() ��������
������Ч��![]() �����ø����ǹ�ʽ�����Һ��������ʣ�������ô𰸣�
�����ø����ǹ�ʽ�����Һ��������ʣ�������ô𰸣�
��1����![]() λ�ڻ�
λ�ڻ�![]() ���е㣬��
���е㣬��![]() λ��
λ��![]() �Ľ�ƽ�����ϣ�
�Ľ�ƽ�����ϣ�
��![]() ��
��
![]() ��
��
��![]() ����
����![]() ��
��
![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�
��![]() ��
��
�����ֵ����ܳ���![]() ��
��
��2����![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��![]()
�����Ҷ�����֪��![]() ��
��
![]() ��
��
![]() ��
��
��![]() ��
��
�����ֵ�ÿ���ܲ����ľ�����Ч��![]() ��
��![]()
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
��![]() ʱ��
ʱ��![]() ȡ���ֵ�����ֵΪ
ȡ���ֵ�����ֵΪ![]() ��
��
�����ֵ�ÿ���ܲ����ľ�����Ч�����ԼΪ1222��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ͼ���������ڵĶԳ����ľ���Ϊ
ͼ���������ڵĶԳ����ľ���Ϊ![]() .
.
��1����![]() ��ֵ��
��ֵ��
��2��������![]() ��ͼ����
��ͼ����![]() ������ƽ��
������ƽ��![]() ����λ���Ⱥ��ٽ��õ���ͼ���ϸ���ĺ������Ϊԭ����
����λ���Ⱥ��ٽ��õ���ͼ���ϸ���ĺ������Ϊԭ����![]() ���������겻�䣬�õ�����
���������겻�䣬�õ�����![]() ��ͼ����
��ͼ����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
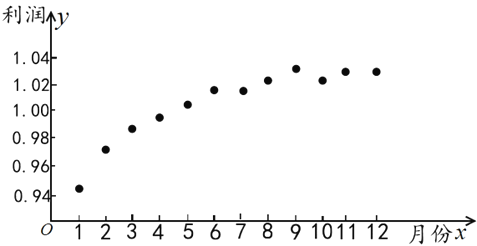
����Ŀ����ͼ��ij��ҵ��˾2017��ÿ�·ݹ�˾����λ������Ԫ�������ɢ��ͼ��Ϊ��Ԥ��ù�˾2018������������������ͼ���ݣ�����������y���·�x���������Իع�ģ�ͣ���![]() 0.94+0.028
0.94+0.028![]() ����
����![]() 0.96+0.032lnx�����õ�����ͳ��ֵ��
0.96+0.032lnx�����õ�����ͳ��ֵ��
ģ�͢� | ģ�͢� | |
�в�ƽ���� | 0.000591 | 0.000164 |
��ƫ��ƽ���� | 0.006050 | |
��1�����������ָ��R2�ж��ĸ�ģ�͵����Ч�����ã�
��2��Ϊ�˼���Ա�������Ļ����ԣ���˾ÿ�»���������������н��ͣ����豾������Ϊy1������һ������Ϊy2������z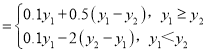 �����涨����z��10������ȫ��Ա�����Ž����ܶ�zԪ����z��10����ȫ��Ա��ÿ�˵Ĺ����е���10��zԪ��Ϊ�ͷ�������Ϊֹ������ݣ�1�������Ч�����õĻع�ģ�ͣ���Ԥ��208��4�·ݸù�˾�Ľ���������������ȷ��С�������λ��
�����涨����z��10������ȫ��Ա�����Ž����ܶ�zԪ����z��10����ȫ��Ա��ÿ�˵Ĺ����е���10��zԪ��Ϊ�ͷ�������Ϊֹ������ݣ�1�������Ч�����õĻع�ģ�ͣ���Ԥ��208��4�·ݸù�˾�Ľ���������������ȷ��С�������λ��
�ο����ݼ���ʽ��![]() 1.73��
1.73��![]() 2.24��1n2��0.69��1n3��1.10��ln5��1.61�����ָ��R2��1
2.24��1n2��0.69��1n3��1.10��ln5��1.61�����ָ��R2��1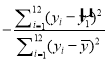 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʯ��ɽ�е�����ѧ�����꼶ͳ��ѧ�������20����ѧ�ܲ�ɼ�������150�֣������м�����λͬѧ��20�γɼ��羥Ҷͼ��ʾ:
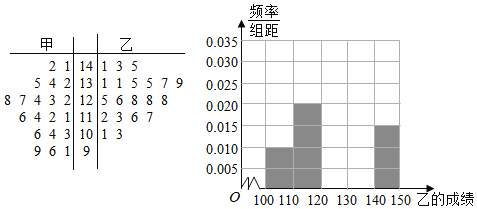
��1�����ݾ�Ҷͼ�������λͬѧ�ɼ�����λ��������ͬѧ�ҵijɼ���Ƶ�ʷֲ�ֱ��ͼ���������
��2�����ݾ�Ҷͼ�Ƚϼ�����λͬѧ��ѧ�ɼ���ƽ��ֵ���ȶ��̶ȣ���Ҫ����������ֵ���������ۼ��ɣ���
��3���ִӼ�����λͬѧ�IJ�����140�ֵijɼ�������ѡ��2���ɼ������¼�![]() Ϊ������2���ɼ��ֱ����ڲ�ͬ��ͬѧ�������¼�
Ϊ������2���ɼ��ֱ����ڲ�ͬ��ͬѧ�������¼�![]() �����ĸ���.
�����ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() ��ֱ��
��ֱ��![]() ������
������![]() ����
����![]() ��
��![]() ����.
����.
��1��������![]() �Ľ��㵽���Ľ�����֮��ľ��룻
�Ľ��㵽���Ľ�����֮��ľ��룻
��2����![]() ����
����![]() �ڵ�һ���ޣ�
�ڵ�һ���ޣ�![]() �ᣬ����Ϊ
�ᣬ����Ϊ![]() ������
������![]() ����ֱ��
����ֱ��![]() ��б�ǵ�ȡֵ��Χ��
��б�ǵ�ȡֵ��Χ��
��3������![]() ����һ��ֱ��
����һ��ֱ��![]() ��
��![]() ������
������![]() ����
����![]() ��
��![]() ���㣬���Ƿ����ʵ��
���㣬���Ƿ����ʵ��![]() ��ʹ��
��ʹ��![]() ��
��![]() ͬʱ������������ڣ��������������ʵ��
ͬʱ������������ڣ��������������ʵ��![]() ��ȡֵ���ϣ���������ڣ���˵������.
��ȡֵ���ϣ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ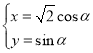 ��
��![]() ������������
Ϊ������������![]() Ϊ���㣬
Ϊ���㣬![]() ��������Ϊ����ļ�����ϵ�У�ֱ��
��������Ϊ����ļ�����ϵ�У�ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��
��
����������![]() ����ͨ���̺�ֱ��
����ͨ���̺�ֱ��![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
�������![]() ����ֱ��
����ֱ��![]() ������
������![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڶ�����![]() �У�����
������![]() ��
��![]() ��
��![]() ��
��![]() ����ƽ��
����ƽ��![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() ��
��![]() .
.
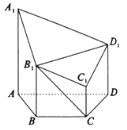
��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2���������![]() �����.
�����.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com