
【题目】已知![]()
(1)求函数![]() 的定义域;
的定义域;
(2)判断函数![]() 的奇偶性,并予以证明。
的奇偶性,并予以证明。
【答案】(1)(-1,1)(2)奇函数
【解析】
(1)由题意可得f(x)﹣g(x)=loga(1+x)﹣loga(1﹣x)=![]() ,由
,由 ![]() 求得函数的定义域;
求得函数的定义域;
(2)由于f(x)﹣g(x)=![]() ,它的定义域为(﹣1,1),令h(x)=f(x)﹣g(x),可得h(﹣x)=﹣h(x),从而得到函数h(x)=f(x)﹣g(x)为奇函数.
,它的定义域为(﹣1,1),令h(x)=f(x)﹣g(x),可得h(﹣x)=﹣h(x),从而得到函数h(x)=f(x)﹣g(x)为奇函数.
(1)由于f(x)=loga(1+x),g(x)=loga(1﹣x),故f(x)﹣g(x)=loga(1+x)﹣loga(1﹣x)=![]() ,
,
由 ![]() ,求得﹣1<x<1,故函数的定义域为(﹣1,1).
,求得﹣1<x<1,故函数的定义域为(﹣1,1).
(2)由于f(x)﹣g(x)=loga(1+x)﹣loga(1﹣x)=![]() ,它的定义域为(﹣1,1),令h(x)=f(x)﹣g(x),
,它的定义域为(﹣1,1),令h(x)=f(x)﹣g(x),
可得h(﹣x)=![]() =﹣
=﹣![]() =﹣h(x),故函数h(x)=f(x)﹣g(x)为奇函数.
=﹣h(x),故函数h(x)=f(x)﹣g(x)为奇函数.


科目:高中数学 来源: 题型:
【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(1)写出价格![]() 关于时间
关于时间![]() 的函数关系式;(
的函数关系式;(![]() 表示投放市场的第
表示投放市场的第![]() 天);
天);
(2)销售量![]() 与时间
与时间![]() 的函数关系:
的函数关系:![]() ,则该产品投放市场第几天销售额最高?最高为多少千元?
,则该产品投放市场第几天销售额最高?最高为多少千元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为{x|x≠0}的偶函数f(x),其导函数为f′(x),对任意正实数x满足xf′(x)>﹣2f(x),若g(x)=x2f(x),则不等式g(x)<g(1﹣x)的解集是( )
A.( ![]() ,+∞)
,+∞)
B.(﹣∞, ![]() )
)
C.(﹣∞,0)∪(0, ![]() )
)
D.(0, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在半径为R的圆桌上摆放同样大小的半径为r的硬币.要求硬币不准露出圆桌面边缘,并且所摆硬币彼此不能重叠.当摆放n枚硬币之后,圆桌上就不能再多摆放一枚这种硬币了.求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某粮库拟建一个储粮仓如图所示,其下部是高为2的圆柱,上部是母线长为2的圆锥,现要设计其底面半径和上部圆锥的高,若设圆锥的高![]() 为
为![]() ,储粮仓的体积为
,储粮仓的体积为![]() .
.
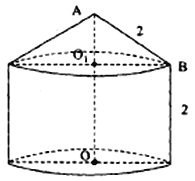
(1)求![]() 关于
关于![]() 的函数关系式;(圆周率用
的函数关系式;(圆周率用![]() 表示)
表示)
(2)求![]() 为何值时,储粮仓的体积最大.
为何值时,储粮仓的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C对边分别为a,b,c,且c<a,已知 ![]() =﹣2,tanB=2
=﹣2,tanB=2 ![]() ,b=3.
,b=3.
(1)求a和c的值;
(2)求sin(B﹣C)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com