
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2)![]() .
.
【解析】
试题分析:(1)法一:过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,由
,由![]() ,推出
,推出![]() ,结合
,结合![]() 与
与![]() ,即可推出四边形
,即可推出四边形![]() 为平行四边形,即可证明结论;法二:过点
为平行四边形,即可证明结论;法二:过点![]() 作
作![]() 于点
于点![]() ,
,![]() 为垂足,连接
为垂足,连接![]() ,由题意,
,由题意,![]() ,则
,则![]() ,即可推出四边形
,即可推出四边形![]() 为平行四边形,再由
为平行四边形,再由![]() 平面
平面![]() ,可推出
,可推出![]() ,即可得证平面
,即可得证平面![]() 平面
平面![]() ,从而得证结论;(2)过
,从而得证结论;(2)过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,结合
,结合![]() 平面
平面![]() ,可推出
,可推出![]() 平面
平面![]() ,由
,由![]() 平面
平面![]() ,可得
,可得![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离,即
的距离,即![]() ,再根据
,再根据![]() ,
,![]() ,即可求出三棱锥
,即可求出三棱锥![]() 的体积.
的体积.
试题解析:(1)法一:过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
∵![]()
∴![]() .
.
又∵![]() ,且
,且![]() ,
,
∴![]() ,∴四边形
,∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() .
.
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
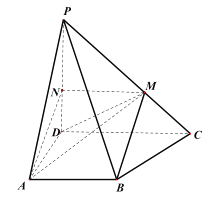
法二:过点![]() 作
作![]() 于点
于点![]() ,
,![]() 为垂足,连接
为垂足,连接![]() .
.
由题意,![]() ,则
,则![]() ,
,
又∵![]() ,
,![]()
∴![]() ,
,
∴四边形![]() 为平行四边形
为平行四边形
∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() .
.
又![]()
∴![]() .
.
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ;
;
∴平面![]() 平面
平面![]() .
.
∵![]() 平面
平面![]()
∴![]() 平面
平面![]() .
.
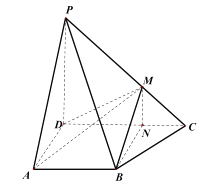
(2)过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() .
.
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ;
;
∴![]() 平面
平面![]()
由(1)知,![]() 平面
平面![]() ,
,
所以![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离,即
的距离,即![]() .
.
在![]() 中,
中,![]() ,
,![]()
∴![]() .
.
![]()
![]() .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|. (Ⅰ)解不等式f(x+8)≥10﹣f(x);
(Ⅱ)若|x|>1,|y|<1,求证:f(y)<|x|f( ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】元旦期间,某轿车销售商为了促销,给出了两种优惠方案,顾客只能选择其中的一种,方案一:每满![]() 万元,可减
万元,可减![]() 千元;方案二:金额超过
千元;方案二:金额超过![]() 万元(含
万元(含![]() 万元),可摇号三次,其规则是依次装有
万元),可摇号三次,其规则是依次装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的一个摇号机,装有
个吉祥号的一个摇号机,装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的二号摇号机,装有
个吉祥号的二号摇号机,装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的三号摇号机各摇号一次,其优惠情况为:若摇出
个吉祥号的三号摇号机各摇号一次,其优惠情况为:若摇出![]() 个幸运号则打
个幸运号则打![]() 折,若摇出
折,若摇出![]() 个幸运号则打
个幸运号则打![]() 折;若摇出
折;若摇出![]() 个幸运号则打
个幸运号则打![]() 折;若没有摇出幸运号则不打折.
折;若没有摇出幸运号则不打折.
(1)若某型号的车正好![]() 万元,两个顾客都选中第二中方案,求至少有一名顾客比选择方案一更优惠的概率;
万元,两个顾客都选中第二中方案,求至少有一名顾客比选择方案一更优惠的概率;
(2)若你评优看中一款价格为![]() 万的便型轿车,请用所学知识帮助你朋友分析一下应选择哪种付款方案.
万的便型轿车,请用所学知识帮助你朋友分析一下应选择哪种付款方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量ξi满足P(ξi=1)=pi , P(ξi=0)=1﹣pi , i=1,2.若0<p1<p2< ![]() ,则( )
,则( )
A.E(ξ1)<E(ξ2),D(ξ1)<D(ξ2)
B.E(ξ1)<E(ξ2),D(ξ1)>D(ξ2)
C.E(ξ1)>E(ξ2),D(ξ1)<D(ξ2)
D.E(ξ1)>E(ξ2),D(ξ1)>D(ξ2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com