已知动圆P与圆M:(x+1)2+y2=16相切,且经过M内的定点N(1,0).
(1)试求动圆的圆心P的轨迹C的方程;
(2)设O是轨迹C上的任意一点(轨迹C与x轴的交点除外),试问在x轴上是否存在两定点A,B,使得直线OA与OB的斜率之积为定值(常数)?若存在,请求出定值,并求出所有满足条件的定点A、B的坐标;若不存在,请说明理由.
分析:(1)利用动圆P与定圆(x-1)2+y2=16相内切,以及椭圆的定义,可得动圆圆心P的轨迹M的方程;
(2)先设任意一点以及A、B的坐标,kQA•kQB=k(常数),根据轨迹方程列出关于k、s、t的方程,并求出k、s、t的值,即可求出结果.
解答:解:(1)由题意,两圆相内切,故,|PM|=4-|PN|,即|PM|+|PN|=4.
又∵MN=2<4
∴动圆的圆心P的轨迹为以M、N为焦点,长轴长为4的椭圆.
动点P的轨迹方程为
+=1.
(2)设点Q(x
0,y
0),则
+=1,x
0≠±2
设A(s,0),B(t,0),k
QA•k
QB=k(常数)
∴k
QA•k
QB=
•===k整理得(4k+3)x
02-4k(s+t)x
0+4(kst-3)=0
由题意,上面的方程对(-2,2)内的一切x
0均成立
∴4k+3=0,-4k(s+t)=0且4(kst-3)=0
解得k=-
,s=2,t=-2,或s=-2,t=2
∴在x轴上只存在两定点A(2,0)、B(-2,0)使得直线QA与QB的斜率之积为定值-
.
点评:题考查圆的基本知识和轨迹方程的求法以及斜率的求法,解题时要注意公式的灵活运用,此题有一定难度.



 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案 且与直线
且与直线 相切.
相切. 与轨迹E交于点A、B,M是线段AB的中点,过M作
与轨迹E交于点A、B,M是线段AB的中点,过M作 轴的垂线交轨迹E于N.
轴的垂线交轨迹E于N. 与AB平行;
与AB平行;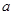 ,使
,使 ?若存在,求
?若存在,求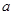 的值;若不存在,说明理由.
的值;若不存在,说明理由.