
����Ŀ��ij��ɴ�������ס���������ɴ����֪����������ɴ1�����һ������2�֡���������1�֣�����������ɴ1�����һ������1�֣���������2�֣�ÿ1�ּ�����ɴ������Ϊ900Ԫ��ÿ1��������ɴ������Ϊ600Ԫ��������������������ɴ�ļƻ��У�Ҫ������һ����������250�֣�������������300�֣��ʼס���������ɴӦ���������ٶ֣���ʹ�����ܶ������������ܶ�����ֵ��
���𰸡��⣺�������ס���������ɴ�ֱ�Ϊx��y�֣������ܶ�Ϊz��
��z=900x+600y
�� 
�������ϲ���ʽ������ʾ��ƽ��������ͼ����
��������
��ֱ��l��900x+600y=0����3x+2y=0��
��ֱ��l�����Ϸ�ƽ������ֱ��2x+y=250��
ֱ��x+2y=300�Ľ���λ��M�� ![]() ��
�� ![]() ����
����
��ʱ���������ܶ�z=900x+600yȡ���ֵ130000Ԫ��
���������������Թ滮֪ʶ��⣬����Լ�������������������ٸ���Ŀ�꺯��z=900x+600y�����ýؾ�ģ�ͣ�ƽ��ֱ���ҵ����Ž⣬���ɣ�


 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д� �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��֪����![]() �IJ�������Ϊ
�IJ�������Ϊ ��
��![]() Ϊ��������������ԭ��
Ϊ��������������ԭ��![]() Ϊ���㣬��
Ϊ���㣬��![]() ���������Ϊ���Ὠ��������ϵ����ֱ֪��
���������Ϊ���Ὠ��������ϵ����ֱ֪��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��
�� ![]() .
.
������ֱ��![]() ������
������![]() ���ڲ�ͬ������
���ڲ�ͬ������![]() ��
�� ![]() ����
����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
����![]() ʱ��������
ʱ��������![]() ����ֱ��
����ֱ��![]() �ԳƵ����߷���.
�ԳƵ����߷���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪{an}�ǵȱ����У�{bn}�ǵȲ����У���a1=b1=1��a1+a2=b4 �� b1+b2=a2 ��
��1����{an}��{bn}��ͨ�ʽ��
��2��������{an+bn}��ǰn���ΪTn �� ��Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�θ��ִ����ϣ���λ��ίΪ���ִ���ķ������£�9.4��8.4��9.4��9.9��9.6��9.4��9.7��ȥ��һ����߷ֺ�һ����ͷֺ���ʣ���ݵ�ƽ��ֵ�ͷ���ֱ�Ϊ�� ��
A.9.4��0.484
B.9.4��0.016
C.9.5��0.04
D.9.5��0.016
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() ��
��
��1����![]() ʱ������
ʱ������![]() �ĵ��������䣻
�ĵ��������䣻
��2���躯��![]() ��
�� ![]() ��������
��������![]() ����Сֵ��
����Сֵ��![]() ����
����![]() ��ֵ��
��ֵ��
��3��������![]() ��
�� ![]() �Ķ�������
�Ķ�������![]() �����ں���
�����ں���![]() ��ͼ���ϵ�����һ��
��ͼ���ϵ�����һ��![]() ���ں���
���ں���![]() ��ͼ���϶�����һ��
��ͼ���϶�����һ��![]() ��ʹ��
��ʹ��![]() ������
������![]() ����Ȼ�����ĵ�����
����Ȼ�����ĵ����� ![]() Ϊ����ԭ������
Ϊ����ԭ������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() .
.
��1�������ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��2�����![]() �ҹ���
�ҹ���![]() �ķ���
�ķ���![]() ������
������![]() ��
�� ![]() ��
��![]() ����֤��
����֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
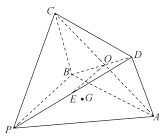
����Ŀ����ͼ��ʾ�ļ�����![]() �У��ı���
�У��ı���![]() Ϊ���Σ�
���� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ��
�� ![]() ��
�� ![]() Ϊ
Ϊ![]() ���е㣬
���е㣬 ![]() Ϊƽ��
Ϊƽ��![]() ����һ��.
����һ��.
��1����ƽ��![]() �ڣ���
�ڣ���![]() ���Ƿ����ֱ��
���Ƿ����ֱ��![]() ʹ
ʹ![]() ����������ڣ���˵�����ɣ�������ڣ���˵��������
����������ڣ���˵�����ɣ�������ڣ���˵��������
��2����![]() ��
�� ![]() ��
�� ![]() �����ƽ�潫������
�����ƽ�潫������![]() ��ȥ����
��ȥ����![]() ����ʣ�༸����
����ʣ�༸����![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ��ax��by+2=0��a��0��b��0����Բx2+y2+4x��4y��1=0���صõ��ҳ�Ϊ6���� ![]() ����СֵΪ�� ��
����СֵΪ�� ��
A.10
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����p��x��A����A={x|a��1��x��a+1}������q��x��B����B={x|x2��4x+3��0}
������A��B=��A��B=R����ʵ��a��ֵ��
������p��q�ij����������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com