
【题目】已知a,b,c为正数,f(x)=|x+a|+|x+b|+|x﹣c|.
(1)若a=b=c=1,求函数f(x)的最小值;
(2)若f(0)=1且a,b,c不全相等,求证:b3c+c3a+a3b>abc.
【答案】(1)最小值2(2)证明见解析
【解析】
(1)法1:去绝对值,化为分段函数,求出最值,
法2:根据绝对值三角不等式,求出最值,
(2)法1:根据基本不等式即可证明,
法2:根据柯西不等式即可证明.
(1)因为a=b=c=1,
所以f(x)=|x+a|+|x+b|+|x﹣c|=2|x+1|+|x﹣1|,
法1:由上可得: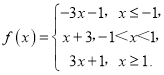
所以,当x=﹣1时,函数f(x)的最小值为2;
法2:f(x)=|x+a|+|x+b|+|x﹣c|=|x+1|+|x+1|+|x﹣1|≥|x+1|+|x+1﹣x+1|=2+|x+1|≥2,
当且仅当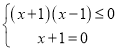 ,即x=﹣1时取得最小值2;
,即x=﹣1时取得最小值2;
(2)因为a,b,c为正数,所以要证b3c+c3a+a3b![]() .,
.,
即证明![]() 就行了,
就行了,
法1:因为![]() 2
2![]() 2
2![]() 2
2![]() 2(a+b+c),当且仅当a=b=c时取等号.
2(a+b+c),当且仅当a=b=c时取等号.
又因为f(0)=1即a+b+c=1且a,b,c不全相等,
所以![]() ,
,
即b3c+c3a+a3b![]() ,
,
法2:因为(a+b+c)![]() ,当且仅当
,当且仅当![]() 取等号,
取等号,
又因为f(0)=1即a+b+c=1且a,b,c不全相等,
所以![]() ,
,
即b3c+c3a+a3b![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P一ABCD中,AB=AD=2BC=2,BC∥AD,AB⊥AD,△PBD为正三角形.且PA=2![]() .
.
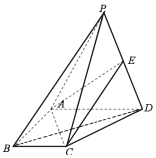
(1)证明:平面PAB⊥平面PBC;
(2)若点P到底面ABCD的距离为2,E是线段PD上一点,且PB∥平面ACE,求四面体A-CDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥S-ABCD中,底面ABCD是边长为2的菱形,![]() ,
,![]() ,二面角S-BD-C的余弦值为
,二面角S-BD-C的余弦值为![]() .
.
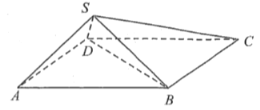
(I)证明:平面![]() 平面SBD;
平面SBD;
(Ⅱ)求二面角A-SD-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥的顶点为A,高和底面的半径相等,BE是底面圆的一条直径,点D为底面圆周上的一点,且∠ABD=60°,则异面直线AB与DE所成角的正弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市在进行创建文明城市的活动中,为了解居民对“创建文明城”的满意程度,组织居民给活动打分(分数为整数,满分100分),从中随机抽取一个容量为120的样本,发现所给数据均在[40,100]内.现将这些分数分成以下6组并画出样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形则下列说法中有错误的是( )
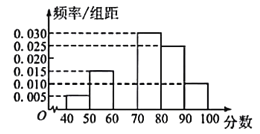
A.第三组的频数为18人
B.根据频率分布直方图估计众数为75分
C.根据频率分布直方图估计样本的平均数为75分
D.根据频率分布直方图估计样本的中位数为75分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果对某对象连续实施两次变换后的结果就是变换前的对象,那么我们称这种变换为“回归”变换.如:对任意一个实数,变换:取其相反数.因为相反数的相反数是它本身,所以变换“取实数的相反数”是一种“回归”变换.有下列3种变换:
①对![]() ,变换:求集合A的补集;
,变换:求集合A的补集;
②对任意![]() ,变换:求z的共轭复数;
,变换:求z的共轭复数;
③对任意![]() ,变换:
,变换:![]() (k,b均为非零实数).
(k,b均为非零实数).
其中是“回归”变换的是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com