
【题目】如图1,已知菱形![]() 的对角线
的对角线![]() 交于点
交于点![]() ,点
,点![]() 为线段
为线段![]() 的中点,
的中点,![]() ,
,![]() ,将三角形
,将三角形![]() 沿线段
沿线段![]() 折起到
折起到![]() 的位置,
的位置,![]() ,如图2所示.
,如图2所示.

(Ⅰ)证明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)见证明;(Ⅱ)![]()
【解析】
(Ⅰ)折叠前,AC⊥DE;,从而折叠后,DE⊥PF,DE⊥CF,由此能证明DE⊥平面PCF.
再由DC∥AE,DC=AE能得到DC∥EB,DC=EB.说明四边形DEBC为平行四边形.可得CB∥DE.由此能证明平面PBC⊥平面PCF.
(Ⅱ)由题意根据勾股定理运算得到![]() ,又由(Ⅰ)的结论得到
,又由(Ⅰ)的结论得到![]()
![]() ,可得
,可得![]() 平面
平面![]() ,再利用等体积转化有
,再利用等体积转化有![]() ,计算结果.
,计算结果.
(Ⅰ)折叠前,因为四边形![]() 为菱形,所以
为菱形,所以![]() ;
;
所以折叠后,![]() ,
,![]() , 又
, 又![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
因为四边形![]() 为菱形,所以
为菱形,所以![]() .
.
又点![]() 为线段
为线段![]() 的中点,所以
的中点,所以![]() .
.
所以四边形![]() 为平行四边形.
为平行四边形.
所以![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(Ⅱ)图1中,由已知得![]() ,
,![]() ,
,![]()
所以图2中,![]() ,又
,又![]()
所以![]() ,所以
,所以![]()
又![]() 平面
平面![]() ,所以
,所以![]()
![]()
又![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() .
.
所以三棱锥![]() 的体积为
的体积为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】问:有多少种不同的方法将集合![]() 中的元素归入
中的元素归入![]() 三个(有序)集合,使得每个元素至少含于其中一个集合之中,这三个集合的交是空集,而其中任两个集合的交都不是空集?
三个(有序)集合,使得每个元素至少含于其中一个集合之中,这三个集合的交是空集,而其中任两个集合的交都不是空集?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
某学校高一数学兴趣小组对学生每周平均体育锻炼小时数与体育成绩优秀(体育成绩满分100分,不低于85分称优秀)人数之间的关系进行分析研究,他们从本校初二,初三,高一,高二,高三年级各随机抽取了40名学生,记录并整理了这些学生周平均体育锻炼小时数与体育成绩优秀人数,得到如下数据表:
初二 | 初三 | 高一 | 高二 | 高三 | |
周平均体育锻炼小时数工(单位:小时) | 14 | 11 | 13 | 12 | 9 |
体育成绩优秀人数y(单位:人) | 35 | 26 | 32 | 26 | 19 |
该兴趣小组确定的研究方案是:先从这5组数据中选取3组数据求线性回归方程,再用剩下的2组数据进行检验.
(1)若选取的是初三,高一,高二的3组数据,请根据这3组数据,求出y关于x的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过1,则认为得到的线性回归方程是可靠的,试问(1)中所得到的线性回归方程是否可靠?
参考数据:![]() ,
,![]() .
.
参考公式: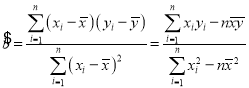 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.

(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)估计该公司投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
销售收益y(单位:万元) | 1 | 3 | 4 | 7 |
表中的数据显示,x与y之间存在线性相关关系,请将(2)的结果填入上表的空白栏,并计算y关于x的回归方程.
回归直线的斜率和截距的最小二乘法估计公式分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 的两顶点
的两顶点![]() ,且点
,且点![]() 满足
满足![]()
(1)求动点![]() 的轨迹方程;
的轨迹方程;![]()
(2)设![]() ,求动点
,求动点![]() 的轨迹方程;
的轨迹方程;
(3)过点![]() 的动直线
的动直线![]() 与曲线
与曲线![]() 交于不同两点
交于不同两点![]() ,过点
,过点![]() 作
作![]() 轴垂线
轴垂线![]() ,试判断直线
,试判断直线![]() 与直线
与直线![]() 的交点是否恒在一条定直线上?若是,求该定直线的方程,否则,说明理由.
的交点是否恒在一条定直线上?若是,求该定直线的方程,否则,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com