
【题目】函数f(x)=|x+1|﹣|2﹣x|.
(1)解不等式f(x)<0;
(2)若m,n∈R+ , ![]() ,求证:n+2m﹣f(x)>0恒成立.
,求证:n+2m﹣f(x)>0恒成立.
【答案】
(1)
解:由f(x)<0得f(x)=|x+1|﹣|2﹣x|<0,即|x+1|<|x﹣2|,
平方得x2+2x+1<x2﹣4x+4,即6x<3,
得x< ![]() ,即不等式的解集为(﹣∞,
,即不等式的解集为(﹣∞, ![]() ).
).
(2)
解:∵n+2m+2=n+1+2m+1=(n+1+2m+1)( ![]() +
+ ![]() )=4+1+
)=4+1+ ![]() +
+ ![]() ≥5+2
≥5+2 ![]() =5+4=9,
=5+4=9,
∴n+2m≥9﹣2=7,当且仅当+ ![]() =
= ![]() ,即n+1=2(2m+1)时取等号,
,即n+1=2(2m+1)时取等号,
∴n+2m的最小值为7,
∵f(x)=|x+1|﹣|2﹣x|≤|x+1+2﹣x|=3,
∴f(x)的最大值为3,
则n+2m>f(x)恒成立,即n+2m﹣f(x)>0恒成立.
【解析】(1)根据绝对值不等式的解法进行求解即可.(2)根据基本不等式的性质,利用1的代换,先求出n+2m的最小值,利用绝对值不等式的性质求出f(x)的最大值,进行比较即可.
【考点精析】掌握基本不等式是解答本题的根本,需要知道基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】某工厂有工人1000名,为了提高工人的生产技能,特组织工人参加培训.其中250名工人参加过短期培训(称为![]() 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为![]() 类工人).现从该工厂的工人中共抽查了100名工人作为样本,调查他们的生产能力(生产能力是指工人一天加工的零件数),得到
类工人).现从该工厂的工人中共抽查了100名工人作为样本,调查他们的生产能力(生产能力是指工人一天加工的零件数),得到![]() 类工人生产能力的茎叶图(图1),
类工人生产能力的茎叶图(图1),![]() 类工人生产能力的频率分布直方图(图2).
类工人生产能力的频率分布直方图(图2).
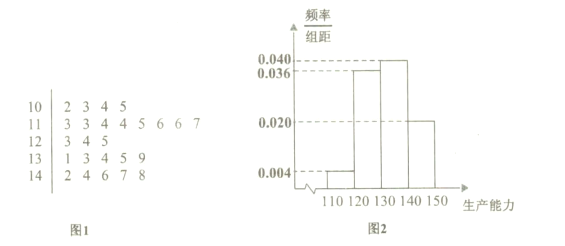
(1)在样本中求![]() 类工人生产能力的中位数,并估计
类工人生产能力的中位数,并估计![]() 类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
(2)若规定生产能力在![]() 内为能力优秀,现以样本中频率作为概率,从1000名工人中按分层抽样共抽取
内为能力优秀,现以样本中频率作为概率,从1000名工人中按分层抽样共抽取![]() 名工人进行调查,请估计这
名工人进行调查,请估计这![]() 名工人中的各类人数,完成下面的
名工人中的各类人数,完成下面的![]() 列联表.
列联表.

若研究得到在犯错误的概率不超过![]() 的前提下,认为生产能力与培训时间长短有关,则
的前提下,认为生产能力与培训时间长短有关,则![]() 的最小值为多少?
的最小值为多少?
参考数据:

参考公式: 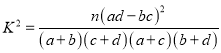 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的右焦点为F(1,0),且点P(1,
=1(a>b>0)的右焦点为F(1,0),且点P(1, ![]() )在椭圆C上,O为坐标原点.
)在椭圆C上,O为坐标原点.
(1)求椭圆C的标准方程;
(2)设过定点T(0,2)的直线l与椭圆C交于不同的两点A、B,且∠AOB为锐角,求直线l的斜率k的取值范围;
(3)过椭圆C1: ![]() +
+ ![]() =1上异于其顶点的任一点P,作圆O:x2+y2=
=1上异于其顶点的任一点P,作圆O:x2+y2= ![]() 的两条切线,切点分别为M,N(M,N不在坐标轴上),若直线MN在x轴、y轴上的截距分别为m、n,证明:
的两条切线,切点分别为M,N(M,N不在坐标轴上),若直线MN在x轴、y轴上的截距分别为m、n,证明: ![]() +
+ ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆O是△ABC的外接圆,∠BAC的平分线交BC于点F,D是AF的延长线与⊙O的交点,AC的延线与⊙O的切线DE交于点E. 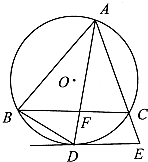
(1)求证: ![]() =
= ![]()
(2)若BD=3 ![]() ,EC=2,CA=6,求BF的值.
,EC=2,CA=6,求BF的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足an+1+an=104n﹣1(n∈N*),数列{bn}的前n项和为Sn , 且bn=log2an .
(1)求bn , Sn;
(2)设cn= ![]() ,证明:
,证明: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() Sn+1(n∈N*).
Sn+1(n∈N*).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com