
【题目】以下说法中,正确的是_____.(填上所有正确说法的序号):
①已知角![]() 终边上一点
终边上一点![]() ,则
,则![]() ;
;
②函数![]() 的最小正周期是
的最小正周期是![]() ;
;
③把函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到
个单位长度可以得到![]() 的图象;
的图象;
④数![]() 的图象关于
的图象关于![]() 对称;
对称;
⑤函数![]() 在
在![]() 上有零点,则实数
上有零点,则实数![]() 的取值范图是
的取值范图是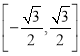 .
.
科目:高中数学 来源: 题型:
【题目】某商场一年购进某种货物900吨,每次都购进x吨,运费为每次9万元,一年的总存储费用为![]() 万元
万元
(1)要使一年的总运费与总存储费用之和最小,则每次购买多少吨?
(2)要使一年的总运费与总存储费用之和不超过585万元,则每次购买量在什么范围?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱拄![]() 中,
中,![]() 侧面
侧面![]() ,已知
,已知![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)试在棱![]() (不包含端点
(不包含端点![]() )上确定一点
)上确定一点![]() 的位置,使得
的位置,使得![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,求![]() 和平面
和平面![]() 所成角正弦值的大小.
所成角正弦值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() .
.
(1)若展开式中奇数项的二项式系数和为128,求展开式中二项式系数最大的项的系数;
(2)若展开式前三项的二项式系数和等于37,求展开式中系数最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】呼和浩特市地铁一号线于2019年12月29日开始正式运营有关部门通过价格听证会,拟定地铁票价后又进行了一次调查.调查随机抽查了50人,他们的月收入情况与对地铁票价格态度如下表:
月收入(单位:百元) |
|
|
|
|
|
|
认为票价合理的人数 | 1 | 2 | 3 | 5 | 3 | 4 |
认为票价偏高的人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)若以区间的中点值作为月收入在该区间内人的人均月收入求参与调查的人员中“认为票价合理者”的月平均收入与“认为票价偏高者”的月平均收入的差是多少(结果保留2位小数);
(2)由以上统计数据填写下面![]() 列联表分析是否有
列联表分析是否有![]() 的把握认为“月收入以5500元为分界点对地铁票价的态度有差异”
的把握认为“月收入以5500元为分界点对地铁票价的态度有差异”
月收入不低于5500元人数 | 月收入低于5500元人数 | 合计 | |
认为票价偏高者 | |||
认为票价合理者 | |||
合计 |
附:![]()
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间中,给出下列说法:①平行于同一个平面的两条直线是平行直线;②垂直于同一条直线的两个平面是平行平面;③若平面![]() 内有不共线的三点到平面
内有不共线的三点到平面![]() 的距离相等,则
的距离相等,则![]() ;④过平面
;④过平面![]() 的一条斜线,有且只有一个平面与平面
的一条斜线,有且只有一个平面与平面![]() 垂直.其中正确的是( )
垂直.其中正确的是( )
A. ①③B. ②④C. ①④D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市由甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同,甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.某公司准备下个月从两家中的一家租一张球台开展活动,活动时间不少于15小时,也不超过40小时,设在甲家租一张球台开展活动![]() 小时的收费为
小时的收费为![]() 元,在乙家租一张球台开展活动
元,在乙家租一张球台开展活动![]() 小时的收费为
小时的收费为![]() 元.
元.
(1)写出![]() 与
与![]() 的解析式;
的解析式;
(2)选择哪家比较合算?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com