
【题目】随着教育信息化2.0时代的到来,依托网络进行线上培训越来越便捷,逐步成为实现全民终身学习的重要支撑.最近某高校继续教育学院采用线上和线下相结合的方式开展了一次300名学员参加的“国学经典诵读”专题培训.为了解参训学员对于线上培训、线下培训的满意程度,学院随机选取了50名学员,将他们分成两组,每组25人,分别对线上、线下两种培训进行满意度测评,根据学员的评分(满分100分)绘制了如下茎叶图:
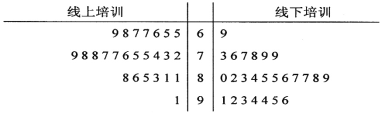
(1)根据茎叶图判断学员对于线上、线下哪种培训的满意度更高?并说明理由;
(2)求50名学员满意度评分的中位数![]() ,并将评分不超过
,并将评分不超过![]() 、超过
、超过![]() 分别视为“基本满意”、“非常满意”两个等级.
分别视为“基本满意”、“非常满意”两个等级.
(i)利用样本估计总体的思想,估算本次培训共有多少学员对线上培训非常满意?
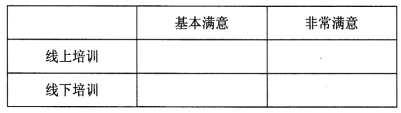
(ii)根据茎叶图填写下面的列联表:
并根据列联表判断能否有99.5%的把握认为学员对两种培训方式的满意度有差异?
附: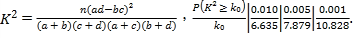
【答案】(1)对线下培训满意度更高(2)(i)![]() 人(ii)有把握
人(ii)有把握
【解析】
(1)由茎叶图,根据中位数、平均数的实际意义,以及数据集中与分散程度可判断哪种培训的满意度更高;(2)(i)直接利用中位数的定义可得中位数![]() 的值,统计对线上培训非常满意的频数可得非常满意的频率,进而可得结果;(ii)根据茎叶图可填写列联表,利用公式求得
的值,统计对线上培训非常满意的频数可得非常满意的频率,进而可得结果;(ii)根据茎叶图可填写列联表,利用公式求得![]() ,与邻界值比较,即可得到结论.
,与邻界值比较,即可得到结论.
(1)对线下培训满意度更高.理由如下:
(i)由茎叶图可知:在线上培训中,有![]() 的学员满意度评分至多
的学员满意度评分至多![]() 分,在线下培训中,有
分,在线下培训中,有![]() 的学员评分至少
的学员评分至少![]() 分.因此学员对线下培训满意度更高.
分.因此学员对线下培训满意度更高.
(ii)由茎叶图可知:线上培训满意度评分的中位数为![]() 分,线下评分的中位数为
分,线下评分的中位数为![]() 分.因此学员对线下培训满意度更高.
分.因此学员对线下培训满意度更高.
(iii)由茎叶图可知:线上培训的满意度评分平均分高于![]() 分;线下培训的平均分低于
分;线下培训的平均分低于![]() 分,因此学员对线下培训满意度更高.
分,因此学员对线下培训满意度更高.
(iv)由茎叶图可知:线上培训的满意度评分在茎![]() 上的最多,关于茎
上的最多,关于茎![]() 大致呈对称分布;线下培训的评分分布在茎
大致呈对称分布;线下培训的评分分布在茎![]() 上的最多,关于茎
上的最多,关于茎![]() 大致呈对称分布,又两种培训方式打分的分布区间相同,故可以认为线下培训评分比线上培训打分更高,因此线下培训的满意度更高.
大致呈对称分布,又两种培训方式打分的分布区间相同,故可以认为线下培训评分比线上培训打分更高,因此线下培训的满意度更高.
以上给出了4种理由,考生答出其中任意一种或其他合理理由均可得分.
(2)由茎叶图知![]() .
.
(i)参加线上培训满意度调查的![]() 名学员中共有
名学员中共有![]() 名对线上培训非常满意,频率为
名对线上培训非常满意,频率为![]() ,
,
又本次培训共![]() 名学员,所以对线上培训满意的学员约为
名学员,所以对线上培训满意的学员约为![]() 人.
人.
(ii)列联表如下:
基本满意 | 非常满意 | |
线上培训 |
|
|
线下培训 |
|
|
于是![]() ,
,
因为![]() ,所以有
,所以有![]() 的把握认为学员对两种培训方式的满意度有差异.
的把握认为学员对两种培训方式的满意度有差异.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】对相关系数r来说,下列说法正确的是( ).
A.![]() ,
,![]() 越接近0,相关程度越大;
越接近0,相关程度越大;![]() 越接近1,相关程度越小
越接近1,相关程度越小
B.![]() ,
,![]() 越接近1,相关程度越大;
越接近1,相关程度越大;![]() 越大,相关程度越小
越大,相关程度越小
C.![]() ,
,![]() 越接近1,相关程度越大;
越接近1,相关程度越大;![]() 越接近0,相关程度越小
越接近0,相关程度越小
D.![]() ,
,![]() 越接近1,相关程度越小;
越接近1,相关程度越小;![]() 越大,相关程度越大
越大,相关程度越大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年高考刚过,为了解考生对全国2卷数学试卷难度的评价,随机抽取了某学校50名男考生与50名女考生,得到下面的列联表:
非常困难 | 一般 | |
男考生 | 20 | 30 |
女考生 | 40 | 10 |
(1)分别估计该学校男考生、女考生觉得全国2卷数学试卷非常困难的概率;
(2)从该学校随机抽取3名男考生,2名女考生,求恰有4名考生觉得全国2卷数学试卷非常困难的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,统计了他们的成绩,得到如图所示的频率分布直方图.
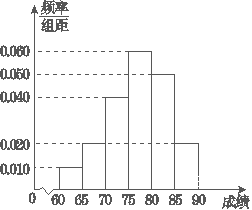
(1)在这个调查采样中,采用的是什么抽样方法?
(2)估计这次测试中优秀(80分及以上)的人数;
(3)写出这40名考生成绩的众数、中位数、平均数的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是国家统计局今年4月11日发布的2018年3月到2019年3月全国居民消费价格的涨跌幅情况折线图.(注:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比),根据该折线图,下列结论错误的是

A. 2018年3月至2019年3月全国居民消费价格同比均上涨
B. 2018年3月至2019年3月全国居民消费价格环比有涨有跌
C. 2019年3月全国居民消费价格同比涨幅最大
D. 2019年3月全国居民消费价格环比变化最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]:在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (t为参数,
(t为参数,![]() ),以坐标原点为极点,以x轴的非负半轴为极轴,建立极坐标系,曲线C的极坐标方程为
),以坐标原点为极点,以x轴的非负半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() ,已知直线
,已知直线![]() 与曲线C交于不同的两点A,B.
与曲线C交于不同的两点A,B.
(1)求直线![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)设P(1,2),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种大型医疗检查机器生产商,对一次性购买2台机器的客户,推出两种超过质保期后两年内的延保维修优惠方案:方案一:交纳延保金7000元,在延保的两年内可免费维修2次,超过2次每次收取维修费2000元;方案二:交纳延保金10000元,在延保的两年内可免费维修4次,超过4次每次收取维修费1000元.某医院准备一次性购买2台这种机器。现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了50台这种机器超过质保期后延保两年内维修的次数,得下表:
维修次数 | 0 | 1 | 2 | 3 |
台数 | 5 | 10 | 20 | 15 |
以这50台机器维修次数的频率代替1台机器维修次数发生的概率,记X表示这2台机器超过质保期后延保的两年内共需维修的次数。
(1)求X的分布列;
(2)以所需延保金及维修费用的期望值为决策依据,医院选择哪种延保方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,上顶点为
,上顶点为![]() ,过
,过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() .当
.当![]() 与
与![]() 重合时,
重合时,![]() 与
与![]() 的面积分别为
的面积分别为![]() 、
、![]() .
.
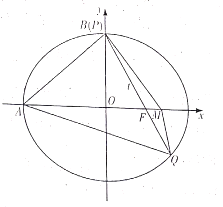
(1)求椭圆![]() 的方程;
的方程;
(2)在![]() 轴上找一点
轴上找一点![]() ,当
,当![]() 变化时,
变化时,![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com