
【题目】如图所示,在三棱柱ABC-A1B1C1中,△ABC与△A1B1C1都为正三角形且AA1⊥面ABC,F、F1分别是AC,A1C1的中点.

求证:(1)平面AB1F1∥平面C1BF;
(2)平面AB1F1⊥平面ACC1A1.
科目:高中数学 来源: 题型:
【题目】三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=![]() ,AB=
,AB=![]() ,AC=2,A1C1=1,
,AC=2,A1C1=1,![]() .
.
(1)证明:BC![]() A1D;
A1D;
(2)求二面角A-CC1-B的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
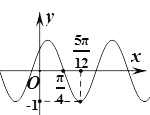
【题目】函数![]() (其中
(其中![]() )的部分图象如图所示,为了得到
)的部分图象如图所示,为了得到![]() 的图象,只要将
的图象,只要将![]() 的图象
的图象
A. 先向右平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
B. 先向右平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
C. 先向左平移![]() 个单位长度 ,再把所得各点的横坐标缩短到原来的
个单位长度 ,再把所得各点的横坐标缩短到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
D. 先向左平移![]() 个单位长度, 再把所得各点的横坐标缩短到原来的
个单位长度, 再把所得各点的横坐标缩短到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一家庭今年一月份、二月份和三月份煤气用量和支付费用如下表所示:
月份 | 用气量(立方米) | 煤气费(元) |
1 | 4 | 4.00 |
2 | 25 | 14.00 |
3 | 35 | 19.00 |
该市煤气收费的方法是:煤气费=基本费+超额费+保险费.
若每月用气量不超过最低额度A(A>4)立方米时,只付基本费3元和每户每月定额保险费C(0<C≤5)元;若用气量超过A立方米时,超过部分每立方米付B元.
(1)根据上面的表格求A,B,C的值;
(2)记该家庭第四月份用气为x立方米,求应交的煤气费y元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球
(Ⅰ)试问:一共有多少种不同的结果?请列出所有可能的结果;
(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2017年8月18日某省x个监测点数据统计如下:
空气污染指数(单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
监测点个数 | 15 | 40 | y | 10 |

(1)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(2)在空气污染指数分别为50~100和150~200的监测点中,用分层抽样的方法抽取5个监测点,从中任意选取2个监测点,事件A“两个都为良”发生的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com