若向量$\overrightarrow{a}$.$\overrightarrow{b}$满足$\overrightarrow{a}$=(1.2).$\overrightarrow{b}$=.则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角等于( )A．$\frac{π}{4}$B．$\frac{π}{3}$C．$\frac{2π}{3}$D� 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

15．若向量$\overrightarrow{a}$、$\overrightarrow{b}$满足$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（1，-3），则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角等于（　　）

A．

$\frac{π}{4}$

B．

$\frac{π}{3}$

C．

$\frac{2π}{3}$

D．

$\frac{3π}{4}$

分析求出$\overrightarrow{a}•\overrightarrow{b}$，|$\overrightarrow{a}$|，|$\overrightarrow{b}$|，代入夹角公式计算．

解答解：$\overrightarrow{a}•\overrightarrow{b}$=1-6=-5，|$\overrightarrow{a}$|=$\sqrt{5}$，|$\overrightarrow{b}$|=$\sqrt{10}$，
∴cos＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=-$\frac{\sqrt{2}}{2}$．
∴向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角等于$\frac{3π}{4}$．
故选D．

点评本题考查了平面向量的数量积运算，是基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

5．已知f（x）是定义在R上的奇函数，f（x+1）是偶函数，当x∈（2，4）时，f（x）=|x-3|，则f（1）+f（2）+f（3）+f（4）=（　　）

A．

B．

C．

D．

-2

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

6．将直径为2的半圆绕直径所在的直线旋转半周而形成的曲面所围成的几何体的表面积为（　　）

A．

2π

B．

3π

C．

4π

D．

6π

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

3．给出下列四个命题：
（1）方程x²+y²-2x-1=0表示的是圆；
（2）动点到两个定点的距离之和为一定长，则动点的轨迹为椭圆；
（3）抛物线x=2y²的焦点坐标是$（{\frac{1}{8}，0}）$；
（4）若双曲线$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{k}$=1的离心率为e，且1＜a＜2，则k的取值范围是k∈（-12，0）
其中正确命题的序号是（1）（3）（4）．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

10．

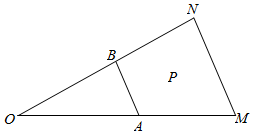如图，在△OMN中，A，B分别是OM，ON中点，若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$（x，y∈R），且点P落在四边形ABNM内（含边界），则x²+y²的取值范围是（　　）

A．

[1，2]

B．

[1，4]

C．

$[\frac{1}{2}，1]$

D．

$[\frac{1}{2}，4]$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

20．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）过点（{1，\frac{{\sqrt{6}}}{3}}）$，离心率为$\frac{{\sqrt{6}}}{3}$．
（I）求椭圆C的标准方程；
（Ⅱ）设椭圆C的下顶点为A，直线l过定点$Q（{0，\frac{3}{2}}）$，与椭圆交于两个不同的点M、N，且满足|AM|=|AN|．求直线l的方程．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

7．抛物线y²=4x上一点P到它的焦点F的距离为5，O为坐标原点，则△PFO的面积为（　　）

A．

B．

$\frac{3}{2}$

C．

D．

$\frac{5}{2}$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

4．已知奇函数f（x）在定义域[-2，2]上单调递减，求满足f（1-m）+f（1-m²）＜0的实数m的取值范围．