【题目】下列说法：
①频率是反映事件发生的频繁程度，概率是反映事件发生的可能性大小；
②百分率是频率，但不是概率；
③频率是不能脱离试验次数
的实验值，而概率是具有确定性的不依赖于试验次数的理论值；
④频率是概率的近似值，概率是频率的稳定值.
其中正确的是______________.
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案科目：高中数学 来源： 题型：
【题目】设数列
的首项为
，前
项和为
，若对任意的
，均有
（
是常数且
）成立，则称数列
为“
数列”.
（1）若数列
为“
数列”，求数列
的通项公式；
（2）是否存在数列
既是“
数列”，也是“
数列”？若存在，求出符合条件的数列
的通项公式及对应的
的值；若不存在，请说明理由；
（3）若数列
为“
数列”， 
，设
，证明： 
.
查看答案和解析>>
科目：高中数学 来源： 题型：
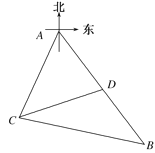
【题目】某观测站
在目标
的南偏西
方向，从
出发有一条南偏东
走向的公路，在
处测得与
相距
的公路
处有一个人正沿着此公路向
走去，走
到达
，此时测得
距离为
，若此人必须在
分钟内从
处到达
处，则此人的最小速度为( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知椭圆
过点
，离心率为
.
分别是椭圆
的上、下顶点，
是椭圆上异于的一点.
（1）求椭圆的方程；
（2）若点
在直线
上，且
，求
的面积；
（3）过点作斜率为
的直线分别交椭圆于另一点
，交
轴于点
，且点在线段
上（不包括端点
），直线
与直线
交于点，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从1，2，3，4，5，6，7，8，9这9个数字中任取两个数，分别有下列事件：
①恰有一个是奇数和恰有一个是偶数；
②至少有一个是奇数和两个数都是奇数；
③至少有一个是奇数和两个数都是偶数；
④至少有一个是奇数和至少有一个是偶数.
其中，为互斥事件的是（ ）
A.①B.②④C.③D.①③
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率.
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)是定义域为R的奇函数，当x<0时，
.
(1)求f(2)的值；
(2)用定义法判断y＝f(x)在区间(－∞，0）上的单调性．
(3)求
的解析式
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】绵阳是党中央、国务院批准建设的中国唯一的科技城，重要的国防科研和电子工业生产基地，市某科研单位在研发过程中发现了一种新合金材料，由大数据测得该产品的性能指标值
（值越大产品的性能越好）与这种新合金材料的含量
（单位：克）的关系为：当
时，是的二次函数；当
时，
测得部分数据如表：
|
|
|
|
|
|
|
|
|
|
|
|
（1）求关于的函数关系式
；
（2）求该新合金材料的含量为何值时产品的性能达到最佳．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若数列{an}是公差为2的等差数列，数列{bn}满足b1＝1，b2＝2，且anbn＋bn＝nbn＋1.
(1)求数列{an}，{bn}的通项公式；
(2)设数列{cn}满足
，数列{cn}的前n项和为Tn，若不等式(－1)nλ<Tn＋
对一切n∈N*恒成立，求实数λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
