解:(Ⅰ)当x≤1时,由f′(x)=-2x+1=0得x=

;
当x>1时,f′(x)=

>0
列表:

∴f(x)的单调增区间为(-∞,

),(1,+∞);
单调减区间为(

,1).
f(x)的极大值为f(

)=

,极小值为f(1)=0.
(Ⅱ)∵x
1<1∴f′(x
1)=-2x
1+1
∴直线PQ的方程为y-f(x
1)=f′(x
1)(x-x
1)
即y-(-x
12+x
1)=(-2x
1+1)(x-x
1),y=(-2x
1+1)x+x
12①
∵x
2>1∴f′(x
2)=

∴直线PQ的方程为y-f(x
2)=f′(x
2)(x-x
2)
即y-lnx
2=

(x-x
2),y=

x+lnx
2-1②
∵①②表示同一条直线方程,∴

消去x
1,得[

(1-

)]
2=lnx
2-1,即

-

-4lnx
2+5=0
令φ(x)=

-

-4lnx+5(x>1),则x
2是φ(x)图象与x轴交点的横坐标.
∵当x>1时,φ′(x)=-

∴φ(x)在(1,+∞)上是减函数
又φ(3)=

φ(4)=

∴3<x
2<4
(Ⅲ)设函数g(x)的定义域为D,区间I⊆D,若函数g(x)在I上可导,对任意的x
0∈I,g(x)的图象在(x
0,g(x
0))处的切线为l,函数g(x)图象上所有的点都在直线l下方或直线l上,则称区间I为函数g(x)的“上线区间”,
所以(-∞,

)不是函数f(x)的“上线区间”.
分析:(Ⅰ)分别当x小于等于1求出f′(x)=0时x的值,然后利用x的值和x=1分区间讨论导函数的正负即可得到函数的单调区间,而当x大于1时得到导函数恒大于0得到函数的增区间,根据函数的增减性得到函数的极值即可;
(Ⅱ)当x
1<1时求出f′(x
1)即为直线PQ的斜率,根据直线PQ过(x
1,f(x
1))和求出的f′(x
1)值写出直线PQ的方程①,当x
2>1时求出f′(x
2)即为直线PQ的斜率,根据直线PQ过(x
2,f(x
2))和求出的f′(x
2)的值写出直线PQ的方程②,因为两条直线表示同一条直线,所以联立①②消去x
1,得到关于x
2的关系式,令φ(x)等于这个关系式,则x
2是φ(x)图象与x轴交点的横坐标.当x大于1时求出φ′(x)判断其值小于0即φ(x)为减函数,因为φ(3)大于0,而φ(4)小于0,所以3<x
2<4得证;
(Ⅲ)由(Ⅱ)可知-2x
1+1=

∈(

,

),∴x
1∈(

,

),再结合f(x)图象得结论.
点评:本题要求学生会根据导函数的正负得到函数的单调区间以及会根据函数的增减性得到函数的极值,在实际问题中掌握导数所表示的意义,是一道中档题.

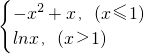 ,
, )是否是函数f(x)的“上线区间”(不必证明).
)是否是函数f(x)的“上线区间”(不必证明). ;
; >0
>0
 ),(1,+∞);
),(1,+∞); ,1).
,1). )=
)= ,极小值为f(1)=0.
,极小值为f(1)=0.
 (x-x2),y=
(x-x2),y= x+lnx2-1②
x+lnx2-1②
 (1-
(1- )]2=lnx2-1,即
)]2=lnx2-1,即 -
- -4lnx2+5=0
-4lnx2+5=0 -
- -4lnx+5(x>1),则x2是φ(x)图象与x轴交点的横坐标.
-4lnx+5(x>1),则x2是φ(x)图象与x轴交点的横坐标.


 )不是函数f(x)的“上线区间”.
)不是函数f(x)的“上线区间”. ∈(
∈( ,
, ),∴x1∈(
),∴x1∈( ,
, ),再结合f(x)图象得结论.
),再结合f(x)图象得结论.

 阅读快车系列答案
阅读快车系列答案