
分析 三棱锥A-BCD的三条侧棱两两互相垂直,所以把它扩展为长方体,它也外接于球,对角线的长为球的直径,然后解答即可.
解答 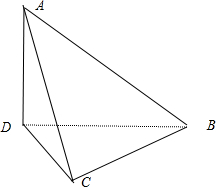 解:∵点A在平面BCD内的投影恰好为点D,∴AD⊥平面BCD,
解:∵点A在平面BCD内的投影恰好为点D,∴AD⊥平面BCD,
故AD=$\sqrt{A{B}^{2}-B{D}^{2}}=\sqrt{7}$,且知AD,BD,CD两两垂直,
故可将此三棱锥放入一个长、宽、高分别为$\sqrt{2}$,$\sqrt{2}$,$\sqrt{7}$的长方体内,三棱锥的四个顶点亦为长方体的顶点,其外接球为长方体外接球.
易得外接球半径为$\frac{\sqrt{11}}{2}$,故外接球表面积为11π.
故答案为:11π
点评 本题考查球的表面积,考查学生空间想象能力,解答的关键是构造球的内接长方体.是基础题


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 递增数列 | B. | 递减数列 | C. | 摆动数列 | D. | 常数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
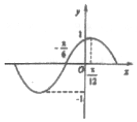 函数f(x)=sin(ωx+φ)(ω<0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.
函数f(x)=sin(ωx+φ)(ω<0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 温度x(℃) | 32 | 33 | 35 | 37 | 38 |
| 西瓜个数y | 20 | 22 | 24 | 30 | 34 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com