练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在①．1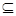{0，1，2,3}；②．{1}∈{0，1，2,3}；③．{0，1，2,3}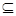{0，1，2,3}；

    ④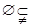．{0}上述四个关系中，错误的个数是：                                        （    ）

    A．1个                        B．2个                    C．3个                       D．4个

     

     

    【答案】

    B

    【解析】①．②错误. 故选B

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    3、设f（x）=x3+x-8，现用二分法求方程x3+x-8=0在区间（1，2）内的近似解，计算得f（1）＜0，f（1.5）＜0，f（1.75）＜0，f（2）＞0，则方程的根所在的区间是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    4x
    x2+a
    ．
    在探究a=1时，函数f（x）在区间[0，+∞）上的最大值问题．为此，我们列表如下
    y 0 0.1 0.2 0.5 0.8 1 1.2 1.5 1.8 2 4 6 …
    y 0 0.396 0.769 1.6 1.951 2 1.967 1.846 1.698 1.6 0.941 0.649 …
    请观察表中y值随x值变化的特点，解答以下两个问题．
    （1）写出函数f（x）在[0，+∞）（a=1）上的单调区间；指出在各个区间上的单调性，并对其中一个区间的单调性用定义加以证明．
    （2）写出函数f（x）（a=1）的定义域，并求f（x）值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在下列各式中错误的个数是（　　）
    ①1∈{0，1，2}；②{1}∈{0，1，2}；③{0，1，2}⊆{0，1，2}；④{0，1，2}={2，0，1}．

    查看答案和解析>>

    科目：高中数学 来源：2008年高考预测卷数学科(一)新课标 题型：044

    已知函数y＝f(x)满足：；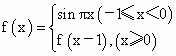

    (1)分别写出x∈[0，1)时y＝f(x)的解析式f1(x)和x∈[1，2)时y＝f(x)的解析式f2(x)；并猜想x∈[n，n＋1)，n≥－1，n∈Z时y＝f(x)的解析式fn+1(x)(用x和n表示)(不必证明)

    (2)当(n≥－1，n∈Z)时，y＝fn+1(x)x∈[n，n＋1)，n≥－1，n∈Z的图象上有点列An+1(x，f(x))和点列Bn+1(n＋1，f(n＋1))，线段An+1Bn+2与线段Bn+1＋An+2的交点Cn+1，求点Cn+1的坐标(an+1(x)，bn+1(x))；

    (3)在前面(1)(2)的基础上，请你提出一个点列Cn+1(an+1(x)，bn+1(x))的问题，并进行研究，并写下你研究的过程

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    继“三鹿奶粉”，“瘦肉精”，“地沟油”等事件的发生之后，食品安全问题屡屡发生，引起了国务院的高度重视．为了加强食品的安全，某食品安检部门调查一个海水养殖场的养殖鱼的有关情况，安检人员从这个海水养殖场中不同位置共捕捞出100条鱼，称得每条鱼的重量（单位：kg），并将所得数据进行统计得下表．若规定超过正常生长的速度为1.0～1.2kg/年的比重超过15%，则认为所饲养的鱼有问题，否则认为所饲养的鱼没有问题．
    鱼的质量[1.00，1.05）[1.05，1.1）[1.10，1.15）[1.15，1.2）[1.20，1.25）[1.25，1.30）
    鱼的条数320353192
    （Ⅰ）根据数据统计表，估计数据落在[1.20，1.30）中的概率约为多少，并判断此养殖场所饲养的鱼是否存在问题？
    （Ⅱ）上面捕捞的100条鱼中间，从重量在[1.00，1.05）和[[1.25，1.30）的鱼中，任取2条鱼来检测，求恰好所取得鱼重量[1.00，1.05）和[[1.25，1.30）各有1条的概率．

    查看答案和解析>>

    同步练习册答案